题目内容
6.已知函数f(x)=cos$\frac{π}{6}x-\sqrt{3}sin\frac{π}{6}$x(0≤x≤5)的图象过点B(4,m),(Ⅰ)若角α的顶点为坐标原点,始边与x轴的非负半轴重合,其终边过点B,求sin2α的值;
(Ⅱ)求函数y=f(x)的最值.
分析 (Ⅰ)把B点坐标代入函数解析式求得m,进而求得sinα和cosα利用二倍角公式求得sin2α的值.
(Ⅱ)利用x的范围确定$\frac{π}{6}$x+$\frac{π}{3}$的范围,利用三角函数图象与性质确定函数的最大和最小值.
解答 解:(Ⅰ)∵函数$f(x)=cos\frac{π}{6}x-\sqrt{3}sin\frac{π}{6}x(0≤x≤5)$的图象过点B(4,m),
∴$m=cos\frac{2π}{3}-\sqrt{3}sin\frac{2π}{3}$=-2,
即点B(4,-2),$|{OB}|=\sqrt{{4^2}+{{(-2)}^2}}=2\sqrt{5}$,
∴$sinα=\frac{-2}{{2\sqrt{5}}}=-\frac{{\sqrt{5}}}{5},cosα=\frac{4}{{2\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$,
∴$sin2α=2sinαcosα=2•({-\frac{{\sqrt{5}}}{5}})•\frac{{2\sqrt{5}}}{5}=-\frac{4}{5}$.
(Ⅱ)$f(x)=2cos(\frac{π}{6}x+\frac{π}{3})$,
∵0≤x≤5,
∴$\frac{π}{3}≤\frac{π}{6}x+\frac{π}{3}≤\frac{7π}{6}$,
当$\frac{π}{6}x+\frac{π}{3}=\frac{π}{3}$时,即x=0时,f(x)max=1,
当$\frac{π}{6}x+\frac{π}{3}=π$时,即x=4时,f(x)min=-2.
点评 本题主要考查了三角函数图象与性质.注意对一些三角函数的定义和公式熟练记忆.

练习册系列答案
相关题目
16.某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某四天的用电量与当天气温,列表如下:
由表中数据得到回归直线方程$\widehat{y}$=-2x+a.据此预测当气温为-4°C时,用电量为68(单位:度).
由表中数据得到回归直线方程$\widehat{y}$=-2x+a.据此预测当气温为-4°C时,用电量为68(单位:度).
| 气温(x℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
1.已知复数z=3+i(i为虚数单位),则z的共轭复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.设f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移φ(φ>0)个单位后,恰好得到函数g(x)=-cos2x-$\sqrt{3}$sin2x的图象,则φ的值可以为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
18.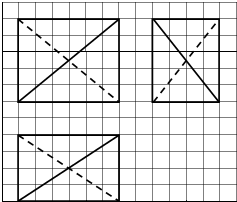 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )| A. | 40cm3 | B. | 50cm3 | C. | 60cm3 | D. | 80cm3 |