题目内容
3．已知集合A={x|-1≤x≤1}，B={x|-1≤x≤a}，且（A∪B）⊆（A∩B），则实数a=（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 由已知中（A∪B）⊆（A∩B），可得：（A∪B）=（A∩B），进而得到A=B，求出实数a的值．
解答 解：∵集合A={x|-1≤x≤1}，B={x|-1≤x≤a}，且（A∪B）⊆（A∩B），
∴（A∪B）=（A∩B），
∴A=B，
∴a=1，
故选：B
点评 本题考查的知识点是集合的交集，并集运算，其中根据已知得到：（A∪B）=（A∩B），进而得到A=B，是解答的关键．
练习册系列答案
相关题目
11．设f（x）=cos2x-$\sqrt{3}$sin2x，把y=f（x）的图象向左平移φ（φ＞0）个单位后，恰好得到函数g（x）=-cos2x-$\sqrt{3}$sin2x的图象，则φ的值可以为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
18．
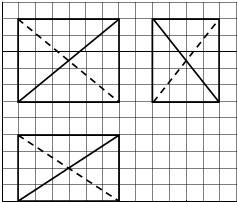如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某多面件的三视图，该多面体的体积为（ ）
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某多面件的三视图，该多面体的体积为（ ）| A． | 40cm3 | B． | 50cm3 | C． | 60cm3 | D． | 80cm3 |
12．若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域存在点（x0，y0）使x0+ay0+2≤0成立，则实数a的取值范围是（ ）
| A． | a＞1 | B． | a＞-1 | C． | a≤1 | D． | a≤-1 |
13．
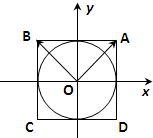如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）
如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 1 |