题目内容
10. 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).(1)求证:MN∥BC;
(2)如果BM⊥AC,求此时$\frac{PM}{PD}$的值.
分析 (1)根据线面平行的性质定理即可证明MN∥BC;
(2)根据线面垂直的判定定理证明BCDK是平行四边形,即可证明M是PD的中点即可得到结论.
解答 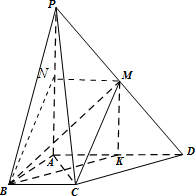 证明:(Ⅰ)∵BC∥AD,BC?平面PAD,AD?平面PAD,
证明:(Ⅰ)∵BC∥AD,BC?平面PAD,AD?平面PAD,
∴BC∥平面PAD,
∵平面PAD∩平面BCMN=MN,
∴BC∥MN,即MN∥BC; …(4分)
(2)过M作MK∥PA交AD于K,则K为AD中点,连结BK.
因为PA⊥底面ABCD,
所以MK⊥底面ABCD.
所以MK⊥AC.
又因为BM⊥AC,BM∩MK=M,
所以AC⊥平面BMK,
所以AC⊥BK.
由K为AD中点,BC∥AD,BC=$\frac{1}{2}$AD,可得DC∥BK,
可得AC⊥CD,
所以在平面ABCD中可得BCDK是平行四边形.
所以BC=DK=AK,
因为K是AD中点,
所以M为PD中点.
所以$\frac{PM}{PD}=\frac{1}{2}$. …(13分)
点评 本题主要考查线面垂直和线面平行的判定和性质,综合考查空间直线和平面的位置关系的判定,要求熟练掌握相应的判定定理和性质定理,考查学生的运算和推理能力,属于基本知识的考查.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
20.若等式(2x-1)2014=a0+a1x+a2x2+…+a2014x2014对于一切实数x都成立,则a0+$\frac{1}{2}a$1+$\frac{1}{3}$a2+…+$\frac{1}{2015}$a2014=( )
| A. | $\frac{1}{4030}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2}{2015}$ | D. | 0 |
1.已知复数z=3+i(i为虚数单位),则z的共轭复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.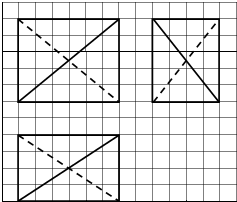 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )| A. | 40cm3 | B. | 50cm3 | C. | 60cm3 | D. | 80cm3 |
2.已知定义在R上的函数f(x)的导函数为f′(x),满足f′(x)<f(x),f(2)=-2,f(1+x)=-f(1-x),则不等式f(x)<2ex的解集为( )
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
19.下列四个函数中,既是奇函数又是定义域上的单调递增的是( )
| A. | y=2-x | B. | y=tanx | C. | y=x3 | D. | y=log3x |