题目内容
5．
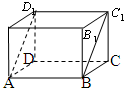如图，在长方体ABCD-A1B1C1D1中，AB=5，BC=4，AA1=3，沿该长方体对角面ABC1D1将其截成两部分，并将它们再拼成一个新的四棱柱，那么这个四棱柱表面积的最大值为114．
分析 根据题目要求，拼成一个新的四棱柱，只能是重合前后，或上下的面，再根据边长得出拼接的几何体，当5×3的两个面叠合时，所得新的四棱柱的表面积最大求解面积即可．
解答 解：根据题目要求得出：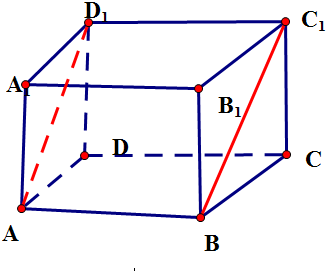
当5×3的两个面叠合时，所得新的四棱柱的表面积最大，其表面积为（5×4+5×5+3×4）×2=114．
故答案为：114
点评 本题考查了空间几何体的性质，运算公式，学生的空间想象能力，属于中档题，难度不大，学会分析判断解决问题．
练习册系列答案
相关题目
16．某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某四天的用电量与当天气温，列表如下：
由表中数据得到回归直线方程$\widehat{y}$=-2x+a．据此预测当气温为-4°C时，用电量为68（单位：度）．
由表中数据得到回归直线方程$\widehat{y}$=-2x+a．据此预测当气温为-4°C时，用电量为68（单位：度）．
| 气温（x℃） | 18 | 13 | 10 | -1 |
| 用电量（度） | 24 | 34 | 38 | 64 |
20．若等式（2x-1）2014=a0+a1x+a2x2+…+a2014x2014对于一切实数x都成立，则a0+$\frac{1}{2}a$1+$\frac{1}{3}$a2+…+$\frac{1}{2015}$a2014=（ ）
| A． | $\frac{1}{4030}$ | B． | $\frac{1}{2015}$ | C． | $\frac{2}{2015}$ | D． | 0 |