题目内容
11．函数f（x）=2xlog2e-2lnx-ax+3的一个极值点在区间（1，2）内，则实数a的取值范围是（0，3）．分析 求导f′（x）=2x-2•$\frac{1}{x}$-a，注意到其在（1，2）上是增函数，故可得f′（1）f′（2）＜0，从而解得．
解答 解：∵f′（x）=2x-2•$\frac{1}{x}$-a在（1，2）上是增函数，
∴若使函数f（x）=2xlog2e-2lnx-ax+3的一个极值点在区间（1，2）内，
则f′（1）f′（2）＜0，
即（-a）（3-a）＜0，
解得，0＜a＜3，
故答案为：（0，3）．
点评 本题考查了导数的综合应用，同时考查了极值的定义，函数的零点存在定理的运用，属于中档题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
1．
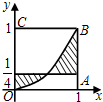如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）
如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
20．我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知F1，F2是一对相关曲线的焦点，P是椭圆和双曲线在第一象限的交点，当∠F1PF2=60°时，这一对相关曲线中椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{1}{2}$ |