题目内容
10．设Sn为等差数列{an}的前n项和，若Sn=$\frac{n}{m}$，Sm=$\frac{m}{n}$（m≠n），则Sm+n-4的符号是（ ）| A． | 正 | B． | 负 | C． | 非负 | D． | 非正 |
分析 利用等差数列的求和公式，求出d=$\frac{2}{mn}$，a1=$\frac{1}{mn}$，再确定Sm+n-4的符号．
解答 解：∵Sn=na1+$\frac{n（n-1）}{2}$d=$\frac{n}{m}$，Sm=ma1+$\frac{m（m-1）}{2}$d=$\frac{m}{n}$，解得d=$\frac{2}{mn}$，a1=$\frac{1}{mn}$．
∵Sm+n-4=（m+n）a1+$\frac{（m+n）（m+n-1）}{2}$d-4=$\frac{{{{（m-n）}^2}}}{mn}$＞0（∵m≠n）．
故选：A．
点评 本题考查等差数列的求和公式，考查学生的计算能力，确定d=$\frac{2}{mn}$，a1=$\frac{1}{mn}$是关键．
练习册系列答案
考前必练系列答案
相关题目
20．在△ABC中，E、F分别为AB、AC上的点，且AE：EB=AF：FC=1：2，P为EF上任一点，实数x、y满足$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$，设△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3，记$\frac{{S}_{1}}{S}$=λ1，$\frac{{S}_{2}}{S}$=λ2，$\frac{{S}_{3}}{S}$=λ3，则当λ2•λ3取最大值时，2x+y的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | 1 | D． | $\frac{3}{2}$ |
1．
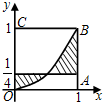如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）
如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
18．已知复数z=1+i+i2+…i10，则复数z在复平面内对应的点为（ ）
| A． | （1，1） | B． | （1，-1） | C． | （0，1） | D． | （1，0） |
15．点P在直径为5的球面上，过P作两两互相垂直的三条弦（两端点均在球面上的线段），若其中一条弦长是另一条弦长的2倍，则这三条弦长之和的最大值是（ ）
| A． | 2$\sqrt{14}$ | B． | 2$\sqrt{70}$ | C． | $\sqrt{70}$ | D． | $\sqrt{14}$ |
20．我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知F1，F2是一对相关曲线的焦点，P是椭圆和双曲线在第一象限的交点，当∠F1PF2=60°时，这一对相关曲线中椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{1}{2}$ |