题目内容
设函数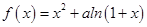 有两个极值点
有两个极值点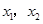 ,且
,且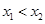 .
.
(1)求 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;
(2)证明: .
.
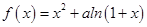 有两个极值点
有两个极值点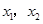 ,且
,且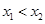 .
.(1)求
 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;(2)证明:
 .
.(1) 的取值范围是
的取值范围是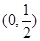
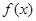 在区间
在区间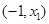 和
和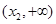 是增函数,在区间
是增函数,在区间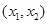 是减函数.
是减函数.
(2)见解析
 的取值范围是
的取值范围是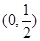
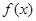 在区间
在区间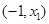 和
和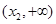 是增函数,在区间
是增函数,在区间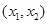 是减函数.
是减函数.(2)见解析
(1)由题设知,函数 的定义域是
的定义域是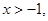
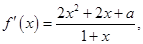
且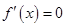 有两个不同的根
有两个不同的根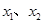 ,故
,故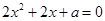 的判别式
的判别式
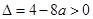 ,
,
即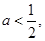
且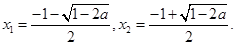 ①
①
又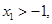 故
故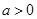 .
.
因此 的取值范围是
的取值范围是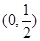 .
.
当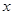 变化时,
变化时,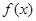 与
与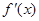 的变化情况如下表:
的变化情况如下表:
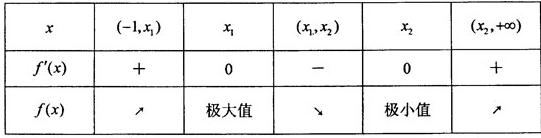
因此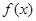 在区间
在区间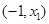 和
和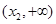 是增函数,在区间
是增函数,在区间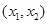 是减函数.
是减函数.
(2)由题设和①知
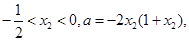
于是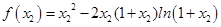 .
.
设函数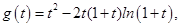
则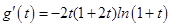
当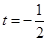 时,
时,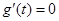 ;
;
当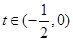 时,
时,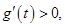 故
故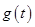 在区间
在区间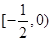 是增函数.
是增函数.
于是,当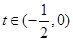 时,
时,
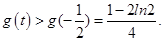
因此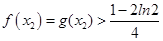 .
.
 的定义域是
的定义域是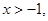
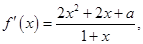
且
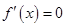 有两个不同的根
有两个不同的根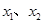 ,故
,故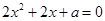 的判别式
的判别式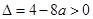 ,
,即
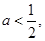
且
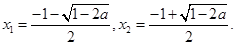 ①
①又
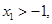 故
故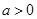 .
.因此
 的取值范围是
的取值范围是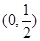 .
.当
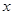 变化时,
变化时,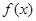 与
与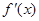 的变化情况如下表:
的变化情况如下表:
因此
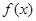 在区间
在区间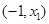 和
和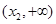 是增函数,在区间
是增函数,在区间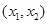 是减函数.
是减函数.(2)由题设和①知
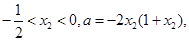
于是
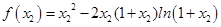 .
.设函数
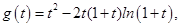
则
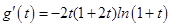
当
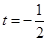 时,
时,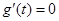 ;
;当
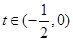 时,
时,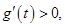 故
故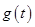 在区间
在区间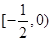 是增函数.
是增函数.于是,当
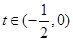 时,
时,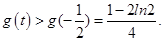
因此
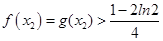 .
.
练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
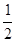
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).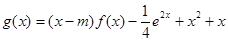 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.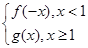 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.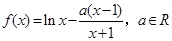 .
.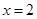 是函数
是函数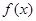 的极值点,求曲线
的极值点,求曲线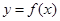 在点
在点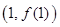 处的切线方程;
处的切线方程;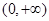 上为单调增函数,求
上为单调增函数,求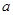 的取值范围.
的取值范围.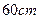 的铁丝分成两段,围成一个正三角形和一个正方形,则正方形的边长为多少时,它和正三角形的面积之和最小。
的铁丝分成两段,围成一个正三角形和一个正方形,则正方形的边长为多少时,它和正三角形的面积之和最小。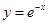 上点
上点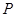 处的切线平行于直线
处的切线平行于直线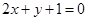 ,则点
,则点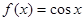 ,
,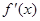 是它的导函数,则
是它的导函数,则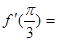 。
。