题目内容
已知函数g(x)="aln" x·f(x)=x3 +x2+bx
(1)若f(x)在区间[1,2]上不是单调函数,求实数b的范围;
(2)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(3)当b=0时,设F(x)=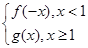 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
(1)若f(x)在区间[1,2]上不是单调函数,求实数b的范围;
(2)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(3)当b=0时,设F(x)=
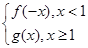 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.(1)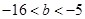 ;(2)
;(2)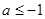 ;(3)详见解析.
;(3)详见解析.
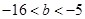 ;(2)
;(2)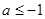 ;(3)详见解析.
;(3)详见解析.试题分析:(1)先求函数的导数,因为在区间
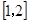 不单调,所以导函数的值不恒大于或小于0,即函数的最大值大于0,函数的最小值小于0,即不单调;
不单调,所以导函数的值不恒大于或小于0,即函数的最大值大于0,函数的最小值小于0,即不单调;(2)根据条件化简
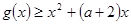 得,
得,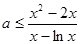 ,
,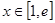 ,求出
,求出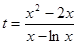 ,
,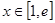 的最小值即可确定
的最小值即可确定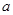 的范围,首先对函数求导,确定单调性,求出最值;
的范围,首先对函数求导,确定单调性,求出最值;(3)先假设曲线
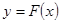 上存在两点
上存在两点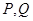 满足题意,设出
满足题意,设出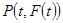
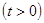 ,则
,则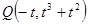 ,从而由
,从而由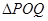 是以O(O为坐标原点)为直角顶点的直角三角形可建立关系式
是以O(O为坐标原点)为直角顶点的直角三角形可建立关系式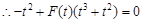 ,分情况求解即可.
,分情况求解即可.试题解析:(1)由
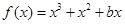
得
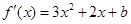 因
因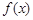 在区间[1,2]上不是单调函数
在区间[1,2]上不是单调函数所以
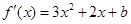 在[1,2]上最大值大于0,最小值小于0
在[1,2]上最大值大于0,最小值小于0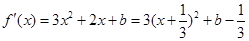
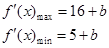 ∴
∴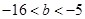 4分
4分(2)由
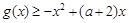 ,得
,得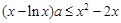 .
.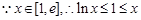 ,且等号不能同时取,
,且等号不能同时取,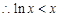 ,即
,即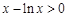
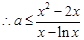 恒成立,即
恒成立,即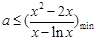 6分
6分令
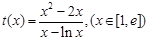 ,求导得,
,求导得,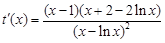 ,
,当
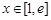 时,
时, ,从而
,从而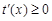 ,
,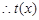 在
在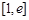 上为增函数,
上为增函数,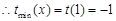 ,
,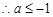 . 8分
. 8分(3)由条件,
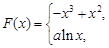
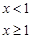 ,
,假设曲线
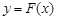 上存在两点
上存在两点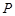 ,
,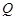 满足题意,则
满足题意,则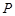 ,
,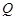 只能在
只能在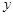 轴两侧, 9分
轴两侧, 9分不妨设
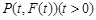 ,则
,则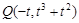 ,且
,且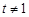 .
.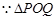 是以
是以 为直角顶点的直角三角形,
为直角顶点的直角三角形,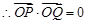 ,
,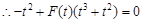 (*),
(*),是否存在
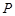 ,
,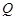 等价于方程
等价于方程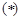 在
在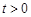 且
且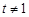 时是否有解.
时是否有解.①若
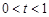 时,方程
时,方程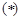 为
为 ,化简得
,化简得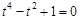 ,此方程无解; 12分
,此方程无解; 12分②若
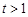 时,方程
时,方程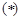 为
为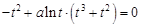 ,即
,即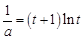 ,
,设
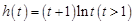 ,则
,则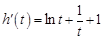 ,
,显然,当
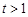 时,
时,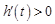 ,即
,即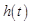 在
在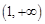 上为增函数,
上为增函数,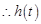 的值域为
的值域为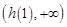 ,即
,即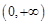 ,
,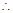 当
当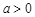 时,方程(*)总有解.
时,方程(*)总有解.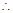 对任意给定的正实数
对任意给定的正实数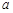 ,曲线
,曲线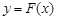 上总存在两点
上总存在两点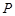 ,
,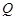 ,使得
,使得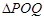 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在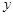 轴上. 14分
轴上. 14分
练习册系列答案
相关题目
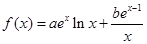 ,曲线
,曲线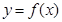 在点
在点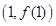 处的切线为
处的切线为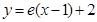 .
.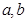 ;
;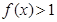 .
.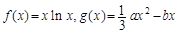 ,其中a,b∈R
,其中a,b∈R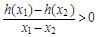 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;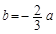 时,若
时,若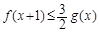 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.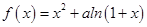 有两个极值点
有两个极值点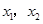 ,且
,且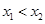 .
. 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性; .
.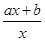 ex,a,b
ex,a,b R,且a>0.
R,且a>0.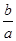 的取值范围.
的取值范围. 的正三棱柱,当它的底面边长为 时,正三棱柱的表面积最小。
的正三棱柱,当它的底面边长为 时,正三棱柱的表面积最小。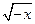 (x
(x 0)的反函数是
0)的反函数是 (x
(x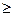 0) (B)
0) (B)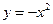 (x
(x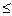 0) (D)
0) (D)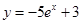 在点
在点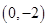 处的切线方程为________.
处的切线方程为________.