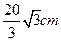题目内容
把边长为 的铁丝分成两段,围成一个正三角形和一个正方形,则正方形的边长为多少时,它和正三角形的面积之和最小。
的铁丝分成两段,围成一个正三角形和一个正方形,则正方形的边长为多少时,它和正三角形的面积之和最小。
 的铁丝分成两段,围成一个正三角形和一个正方形,则正方形的边长为多少时,它和正三角形的面积之和最小。
的铁丝分成两段,围成一个正三角形和一个正方形,则正方形的边长为多少时,它和正三角形的面积之和最小。正方形的边长为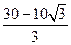
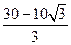
设分成的两段为 ,
,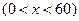 ,则
,则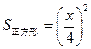 ,
, ,∴
,∴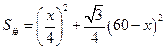
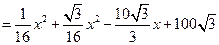 ,∴
,∴ ,∴
,∴ 得
得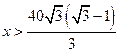 ,∴当
,∴当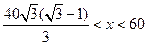 时,
时,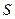 单调递增,当
单调递增,当 时,
时,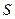 单调递减,∴
单调递减,∴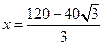 时,
时,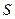 最小,此时正方形的边长为
最小,此时正方形的边长为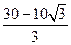 。
。
名师点金:此题的变式比较新颖,真正体现了利用数学知识解决实际问题的思想,将原来的围成矩形改为围成一个矩形和一个正三角形,题目的难度有了显著的提升,在解此变式的过程中,要注意所设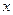 是有范围的,这一点很容易被忽略,另外,此题还可以作其他形状的变式,在此不一一列举。
是有范围的,这一点很容易被忽略,另外,此题还可以作其他形状的变式,在此不一一列举。
 ,
,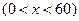 ,则
,则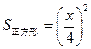 ,
, ,∴
,∴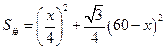
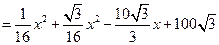 ,∴
,∴ ,∴
,∴ 得
得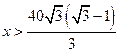 ,∴当
,∴当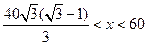 时,
时,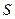 单调递增,当
单调递增,当 时,
时,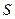 单调递减,∴
单调递减,∴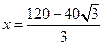 时,
时,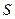 最小,此时正方形的边长为
最小,此时正方形的边长为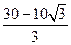 。
。名师点金:此题的变式比较新颖,真正体现了利用数学知识解决实际问题的思想,将原来的围成矩形改为围成一个矩形和一个正三角形,题目的难度有了显著的提升,在解此变式的过程中,要注意所设
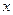 是有范围的,这一点很容易被忽略,另外,此题还可以作其他形状的变式,在此不一一列举。
是有范围的,这一点很容易被忽略,另外,此题还可以作其他形状的变式,在此不一一列举。
练习册系列答案
相关题目
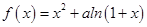 有两个极值点
有两个极值点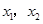 ,且
,且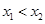 .
. 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性; .
.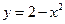 与
与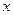 轴所围成图形的最大矩形面积为 。
轴所围成图形的最大矩形面积为 。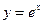 的切线,则切点的坐标为 ,切线的方程为 。
的切线,则切点的坐标为 ,切线的方程为 。 的正三棱柱,当它的底面边长为 时,正三棱柱的表面积最小。
的正三棱柱,当它的底面边长为 时,正三棱柱的表面积最小。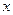 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 万元。(1)试写出
万元。(1)试写出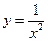 和
和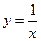 在它们交点处的两切线夹角为
在它们交点处的两切线夹角为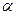 ,求
,求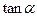 。
。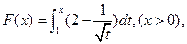 则
则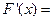 ______.
______.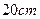 ,要使其体积为最大,则其高为多少厘米( )
,要使其体积为最大,则其高为多少厘米( )