题目内容
已知f(x)是可导的函数,且
=-2,则曲线y=f(x)在点(2,2)处的切线的一般式方程是______.
| lim |
| x→0 |
| f(x+2)-f(2) |
| 2x |
∵
=-2,∴
=-2
=-4,∴f′(2)=-4
∴曲线y=f(x)在点(2,2)处的切线的斜率为-4,
切线方程为y=-4x+10,化为一般式为4x+y-10=0
故答案为4x+y-10=0
| lim |
| x→0 |
| f(x+2)-f(2) |
| 2x |
| 1 |
| 2 |
| lim |
| x→0 |
| f(x+2)-f(2) |
| x |
| lim |
| x→0 |
| f(x+2)-f(2) |
| x |
∴曲线y=f(x)在点(2,2)处的切线的斜率为-4,
切线方程为y=-4x+10,化为一般式为4x+y-10=0
故答案为4x+y-10=0

练习册系列答案
相关题目
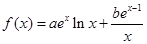 ,曲线
,曲线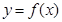 在点
在点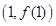 处的切线为
处的切线为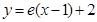 .
.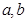 ;
;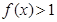 .
.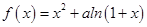 有两个极值点
有两个极值点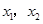 ,且
,且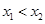 .
. 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性; .
.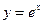 的切线,则切点的坐标为 ,切线的方程为 。
的切线,则切点的坐标为 ,切线的方程为 。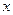 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 万元。(1)试写出
万元。(1)试写出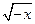 (x
(x 0)的反函数是
0)的反函数是 (x
(x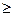 0) (B)
0) (B)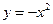 (x
(x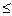 0) (D)
0) (D)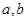 为常数,且
为常数,且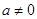 ,函数
,函数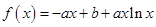 ,
,
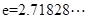 是自然对数的底数).
是自然对数的底数).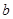 的值;
的值;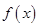 的单调区间;
的单调区间;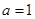 时,是否同时存在实数
时,是否同时存在实数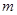 和
和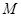 (
(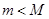 ),使得对每一个
),使得对每一个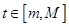 ,直线
,直线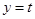 与曲线
与曲线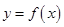
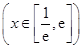 都有公共点?若存在,求出最小的实数
都有公共点?若存在,求出最小的实数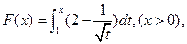 则
则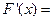 ______.
______.