题目内容
已知函数f(x)=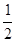
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数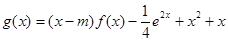 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.
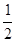
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).(1)讨论函数f(x)的单调性;
(2)若a=1,函数
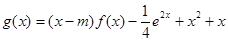 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.(1)当 时,
时, 在
在 上为增函数;当
上为增函数;当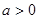 时,
时, 在
在 为减函数,在
为减函数,在 为增函数;(2)
为增函数;(2) 的最大值为1.
的最大值为1.
 时,
时, 在
在 上为增函数;当
上为增函数;当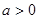 时,
时, 在
在 为减函数,在
为减函数,在 为增函数;(2)
为增函数;(2) 的最大值为1.
的最大值为1.试题分析:(1)讨论函数的单调性首先注意明确函数的定义域,由于该函数是超越函数与一次函数的和构成的,所以考虑用导数,先求出函数的导数得
 ,由指数函数的性质可知要确定导数的正负须按
,由指数函数的性质可知要确定导数的正负须按 和
和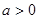 分类讨论,确定导数的符号而求出函数的单调区间;(2)函数
分类讨论,确定导数的符号而求出函数的单调区间;(2)函数 在区间(0,+
在区间(0,+ )上为增函数
)上为增函数 在
在 恒成立,分离参数m,从而将所求问题转化为求函数的最值问题,构造新函数,再用导数研究此函数的最小值即可;注意所求的m为整数这一特性.
恒成立,分离参数m,从而将所求问题转化为求函数的最值问题,构造新函数,再用导数研究此函数的最小值即可;注意所求的m为整数这一特性.试题解析:(1)定义域为
 ,
, ,
,当
 时,
时, ,所以
,所以 在
在 上为增函数; 2分
上为增函数; 2分当
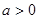 时,由
时,由 得
得 ,且当
,且当 时,
时,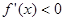 ,
,当
 时
时 ,
,所以
 在
在 为减函数,在
为减函数,在 为增函数. 6分
为增函数. 6分(2)当
 时,
时,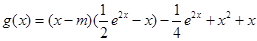 ,
,若
 在区间
在区间 上为增函数,
上为增函数,则
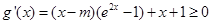 在
在 恒成立,
恒成立,即
 在
在 恒成立 8分
恒成立 8分令
 ,
,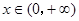 ;
; ,
,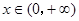 ;令
;令 ,
,可知
 ,
, ,
,又当
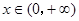 时
时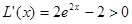 ,
,所以函数
 在
在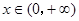 只有一个零点,设为
只有一个零点,设为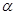 ,即
,即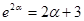 ,
,且
 ; 9分
; 9分由上可知当
 时
时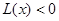 ,即
,即 ;当
;当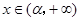 时
时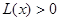 ,即
,即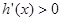 ,
,所以
 ,
,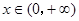 ,有最小值
,有最小值 , 10分
, 10分把
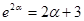 代入上式可得
代入上式可得 ,又因为
,又因为 ,所以
,所以 ,
,又
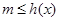 恒成立,所以
恒成立,所以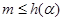 ,又因为
,又因为 为整数,
为整数,所以
 ,所以整数
,所以整数 的最大值为1. 12分
的最大值为1. 12分
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
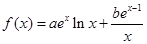 ,曲线
,曲线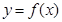 在点
在点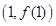 处的切线为
处的切线为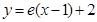 .
.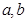 ;
;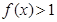 .
.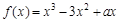
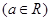 .
.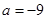 时,求函数
时,求函数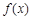 的极大值;
的极大值;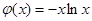 的图象有三个不同的交点,求
的图象有三个不同的交点,求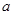 的取值范围;
的取值范围;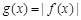 ,当
,当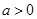 时,求函数
时,求函数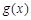 的单调减区间.
的单调减区间.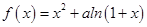 有两个极值点
有两个极值点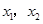 ,且
,且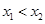 .
. 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性; .
.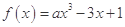 对于
对于 总有
总有
 0 成立,则
0 成立,则 = .
= .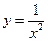 和
和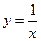 在它们交点处的两切线夹角为
在它们交点处的两切线夹角为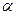 ,求
,求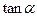 。
。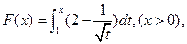 则
则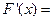 ______.
______.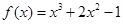 ,则
,则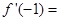 ( )
( )