题目内容
17.一空间几何体的三视图如图所示,则该几何体的体积为$\frac{7}{6}$表面积为$\frac{11+4\sqrt{2}+\sqrt{3}}{2}$
分析 这是一个空间组合体,上面是一个三棱锥,三棱锥的底面是一个直角边是1的直角三角形,高是1,下面是一个三棱柱,三棱柱的底面是一个直角边是1的直角三角形,高是2,得到原几何体后即可求得其体积和表面积.
解答 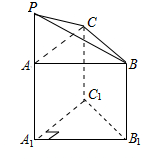 解:由三视图得原几何体如图,
解:由三视图得原几何体如图,
上面是一个三棱锥,三棱锥的底面是一个直角边是1的直角三角形,高是1,下面是一个三棱柱,三棱柱的底面是一个直角边是1的直角三角形,高是2.
∴三棱锥的体积是$\frac{1}{3}$×$\frac{1}{2}$×1×1×1=$\frac{1}{6}$.
下面是一个三棱柱,三棱柱的底面是一个直角边是1的直角三角形,高是2,
∴三棱柱的体积是$\frac{1}{2}$×1×1×2=1.
∴空间几何体的体积是$\frac{1}{6}+1=\frac{7}{6}$;
组合体的表面积为:(1×2+1×2$+\sqrt{2}×2$$+\frac{1}{2}×1×1$)+($\frac{1}{2}×1×1+\frac{1}{2}×1×1$+$\frac{1}{2}×\sqrt{2}×\frac{\sqrt{6}}{2}$)=$\frac{11+4\sqrt{2}+\sqrt{3}}{2}$.
故答案为:$\frac{7}{6}$;$\frac{11+4\sqrt{2}+\sqrt{3}}{2}$.
点评 本题考查由三视图求空间几何体的体积和表面积,由三视图正确还原原几何体是解答该题的关键,是中档题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
5.若集合A={y|y=2x},B={x|x2-2x-3>0,x∈R},那么A∩(∁UB)=( )
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (0,-1)∪(3,+∞) |
12.表面积为S的五面体的每一个面都外切于半径为R的一个球,则这个五面体的体积为( )
| A. | $\frac{1}{3}$SR | B. | $\frac{3}{5}$SR | C. | $\frac{2}{3}$SR | D. | $\frac{3}{2}$SR |
9.已知P:log3(-x2-2x+3)<0,则使得P成立的一个充分不必要条件是( )
| A. | [$\frac{5}{6}$,1) | B. | (-3,1) | C. | (-∞,-$\sqrt{3}$-1)∪($\sqrt{3}$-1,+∞) | D. | (-3,-$\sqrt{3-1)}$∪($\sqrt{3}$-1,1) |
6.函数f(x)=$\frac{1}{lgx}$+$\sqrt{2-x}$ 的定义域为( )
| A. | (-∞,2] | B. | (0,1)∪(1,2) | C. | (0,2] | D. | (0,2) |
