Question

【题目】在平面直角坐标系中,已知三点A(-1,0)、B(t,2)、C(2,1)，t∈R，O为坐标原点

(I)若△ABC是∠B为直角的直角三角形,求t的值

(Ⅱ)若四边形ABCD是平行四边形，求的最小值

Answer 1

【答案】(I)t＝1. (II) .

【解析】试题分析：(1)利用向量垂直解得即可;

(2)由题意得,求得D的坐标D(1－t，t－2),利用求模公式即可得出结论.

试题解析：(I)由题意得＝(t＋1,2)， ＝(3，t)， ＝(2－t，t－2)，

若∠B＝90°，则，即(t＋1) (2－t)＋2(t－2)＝0，∴t＝1或2，

若，则，这时△ABC不存在.∴t＝1.

(II)若四边形ABCD是平行四边形，则，设点D的坐标为(x，y)，

则＝(x＋1,y)，∴(x＋1,y)＝(2－t，t－2)，

∴，即，即D(1－t，t－2)，∴＝(1－t，t－2)，

∴＝＝＝，

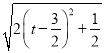∴当t＝时， 取得最小值.