题目内容
【题目】一条光线从点（﹣2，﹣3）射出，经y轴反射后与圆（x+3）2+（y﹣2）2=1相切，则反射光线所在直线的斜率为（ ）
A.﹣ 
或﹣ 
B.﹣ 
或﹣ 
C.﹣ 
或﹣ 
D.﹣ 
或﹣ 
【答案】D
【解析】解：点A（﹣2，﹣3）关于y轴的对称点为A′（2，﹣3），
故可设反射光线所在直线的方程为：y+3=k（x﹣2），化为kx﹣y﹣2k﹣3=0．
∵反射光线与圆（x+3）2+（y﹣2）2=1相切，
∴圆心（﹣3，2）到直线的距离d= 
=1，
化为24k2+50k+24=0，
∴k= 
或﹣ 
．
所以答案是：D．
【考点精析】认真审题，首先需要了解直线的斜率(一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα)．
练习册系列答案
相关题目
【题目】某地区某中草药材的销售量与年份有关，下表是近五年的部分统计数据：
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量（吨） | 114 | 115 | 116 | 116 | 114 |
（1）利用所给数据求年销售量
与年份
之间的回归直线方程
；
（2）利用（1）中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式：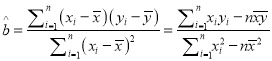 
， 
.
