题目内容
【题目】已知函数 ![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)求证:函数![]() 在
在![]() 为单调增函数;
为单调增函数;
(3)求满足![]() 的
的![]() 的取值范围.
的取值范围.
【答案】(1)![]() 为奇函数;(2)证明见解析;(3)
为奇函数;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(Ⅰ)求出定义域为{x|x≠0且x∈R},关于原点对称,再计算f(-x),与f(x)比较即可得到奇偶性;
(Ⅱ)运用单调性的定义,注意作差、变形、定符号、下结论等步骤;
(Ⅲ)讨论x>0,x<0,求出f(x)的零点,再由单调性即可解得所求取值范围.
试题解析:
(1)定义域为{x|x≠0且x∈R},关于原点对称,
![]() ,所以
,所以![]() 为奇函数;
为奇函数;
(2)任取![]() ,
, 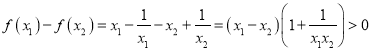
所以![]() 在
在![]() 为单调增函数;
为单调增函数;
(3)![]() 解得
解得![]() ,所以零点为
,所以零点为![]() ,
,
当![]() 时,由(2)可得
时,由(2)可得![]() 的
的![]() 的取值范围为
的取值范围为![]() ,
, ![]() 的
的![]() 的取值范围为
的取值范围为![]() ,又该函数为奇函数,所以当
,又该函数为奇函数,所以当![]() 时,由(2)可得
时,由(2)可得![]() 的
的![]() 的取值范围为
的取值范围为![]() ,
,
综上:所以 ![]() 解集为
解集为![]() .
.

练习册系列答案
相关题目
【题目】某地区某中草药材的销售量与年份有关,下表是近五年的部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量(吨) | 114 | 115 | 116 | 116 | 114 |
(1)利用所给数据求年销售量![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式: 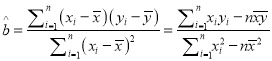 ,
, ![]() .
.