Question

【题目】已知圆C的方程：x2+y2﹣2x﹣4y+m=0
（1）求m的取值范围；
（2）圆C与直线x+2y﹣4=0相交于M，N两点，且OM⊥ON（O为坐标原点），求m的值．

Answer 1

【答案】
（1）解：方程x2+y2﹣2x﹣4y+m=0，

可化为（x﹣1）2+（y﹣2）2=5﹣m，

∵此方程表示圆，

∴5﹣m＞0，即m＜5

（2）解：）

消去x得（4﹣2y）2+y2﹣2×（4﹣2y）﹣4y+m=0，

化简得5y2﹣16y+m+8=0．

∵△=4（24﹣5m）＞0，∴ ，

设M（x1，y1），N（x2，y2），

则 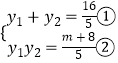，由OM⊥ON得y1y2+x1x2=0，

即y1y2+（4﹣2y1）（4﹣2y2）=0，

∴16﹣8（y1+y2）+5y1y2=0．

将①②两式代入上式得16﹣8× +5× =0，

解之得 符合

【解析】（1）先将圆的一般方程化为圆的标准方程，再求得m的取值范围；（2）本小题的关键在于利用OM⊥ON，则直线OM，直线ON斜率的乘积为-1，从而得到y1y2+x1x2=0这一关系式.
【考点精析】本题主要考查了圆的标准方程和直线与圆的三种位置关系的相关知识点，需要掌握圆的标准方程：；圆心为A(a,b),半径为r的圆的方程；直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．