题目内容
已知数列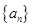 满足
满足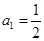 ,
,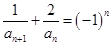
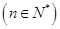 .
.
(1)求证:数列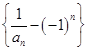
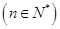 是等比数列;
是等比数列;
(2)设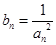
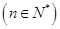 ,求数列
,求数列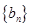 的前
的前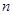 项和
项和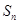 ;
;
(3)设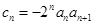 ,数列
,数列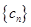 的前
的前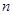 项和为
项和为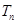 ,求证:
,求证: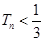 (其中
(其中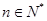 ).
).
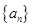 满足
满足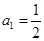 ,
,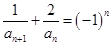
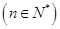 .
.(1)求证:数列
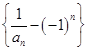
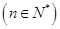 是等比数列;
是等比数列;(2)设
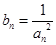
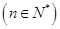 ,求数列
,求数列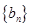 的前
的前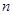 项和
项和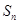 ;
;(3)设
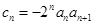 ,数列
,数列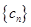 的前
的前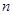 项和为
项和为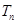 ,求证:
,求证: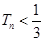 (其中
(其中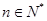 ).
).(1)见解析;(2)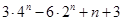 ;(3)见解析.
;(3)见解析.
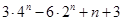 ;(3)见解析.
;(3)见解析.试题分析:(1)首先由
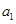 求出
求出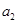 ,然后
,然后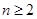 时,构造函数
时,构造函数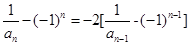 ,即可证明在
,即可证明在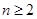 条件下数列
条件下数列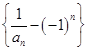
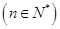 是等比数列,将
是等比数列,将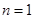 时的值代入也符合,即证;(2)先由(1)得到
时的值代入也符合,即证;(2)先由(1)得到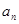 ,然后写出
,然后写出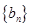 的通项公式,根据等比数列前
的通项公式,根据等比数列前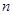 项和公式求出
项和公式求出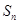 ;(3)求出数列
;(3)求出数列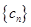 的通项公式,再由累加法求其前
的通项公式,再由累加法求其前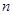 项和为
项和为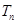 ,再判断
,再判断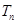 与
与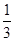 的关系.
的关系.试题解析:(1)证明:由
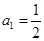 ,
,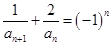 得
得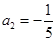 ,
,当
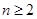 时,
时,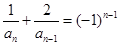 ,即
,即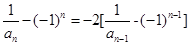 ,
,所以
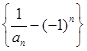 是首项为
是首项为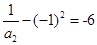 ,公比为
,公比为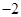 的等比数列,
的等比数列,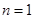 时,也符合,所以数列
时,也符合,所以数列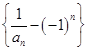
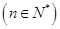 是等比数列; .5分
是等比数列; .5分(2)
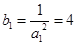 ,由(I)得
,由(I)得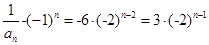 ,所以
,所以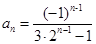 .
.所以
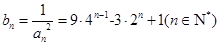 ,
,数列
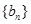 的前n项和
的前n项和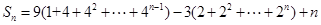
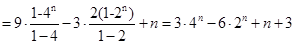 . 10分
. 10分(3)证明:
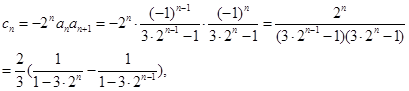
所以,数列
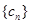 的前n项和为
的前n项和为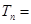
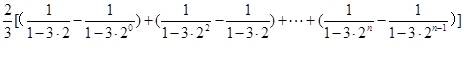
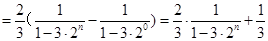
因为当
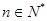 时,
时,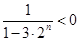 ,所以
,所以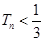 14分
14分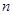 项和;4、累加法求数列的前
项和;4、累加法求数列的前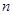 项和.
项和.
练习册系列答案
相关题目
 满足:
满足: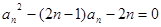 .
.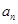 ;
;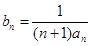 ,求数列
,求数列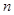 项和
项和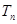 .
.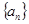 的各项均为正数,其前
的各项均为正数,其前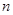 项和为
项和为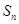 ,且
,且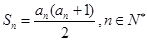 .
.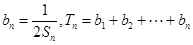 ,求证:
,求证: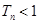 ;
;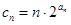 ,
,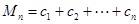 ,求
,求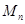 .
.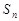 为数列
为数列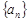 的前
的前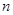 项和,且
项和,且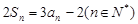 .
.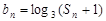 ,求数列
,求数列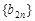 的前n项和
的前n项和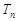 .
.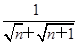 ,若{an}的前n项和为24,则n为________.
,若{an}的前n项和为24,则n为________.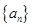 中,
中,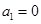 ,
,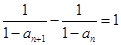 ,设
,设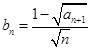 ,记
,记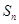 为数列
为数列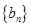 的前
的前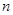 项和,则
项和,则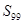 = .
= .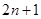 项,其中奇数项和为290,偶数项和为261,则
项,其中奇数项和为290,偶数项和为261,则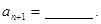
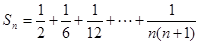 ,且
,且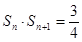 ,则
,则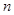 的值为 ( )
的值为 ( )