题目内容
【题目】已知函数
，
的在数集
上都有定义，对于任意的
，当
时，
或
成立，则称是数集上的限制函数.
（1）求
在
上的限制函数的解析式；
（2）证明：如果在区间
上恒为正值，则在
上是增函数；[注：如果在区间上恒为负值，则在区间上是减函数，此结论无需证明，可以直接应用]
（3）利用（2）的结论，求函数
在
上的单调区间.
【答案】（1）
；（2）证明见解析；（3）见解析.
【解析】
（1）由题目给出的条件，构造
，根据条件验证可得所求函数；
（2）运用反证法，即可得证；
（3）求得，根据第二问结论由大于0，可得增区间；小于0，可得减区间．
解：（1）任意的
，
；
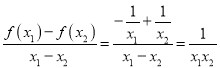由于任意性：
；
故构造；
由幂函数性质得在
单调递减，
且易得：
，满足题意，
故：；
（2）运用反证法，即假设
在
上不是增函数，
若在上是减函数，可得在区间
上恒为负值；
若在上是常数函数，可得在区间上恒为零；
若在上是有增有减，可得在区间上可能为正可能为负；
这与在区间上恒为正值矛盾，故在上是增函数；
（3）任意的
，当
，
，
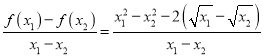
构造
；
任取，
，
，
，
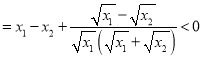故：
，
是数集
上的限制函数，
，解得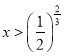
利用（2）结论，当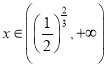
函数单调递增，
，解得
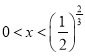
利用（2）结论，当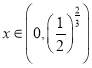
函数单调递减.
练习册系列答案
阅读快车系列答案
相关题目
