题目内容
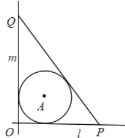
【题目】在直角坐标平面内,直线l过点P(1,1),且倾斜角α=![]() .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A,B两点,求|PA|·|PB|的值.
【答案】(1)x2+y2-4y=0.(2)2
【解析】
试题(1)根据![]() 将圆C的极坐标方程化为直角坐标方程(2)设直线参数方程,与圆方程联立,根据参数几何意义以及韦达定理得|PA|·|PB|=|t1t2|=2.
将圆C的极坐标方程化为直角坐标方程(2)设直线参数方程,与圆方程联立,根据参数几何意义以及韦达定理得|PA|·|PB|=|t1t2|=2.
试题解析:(1)∵ρ=4sin θ,∴ρ2=4ρsin θ,
则x2+y2-4y=0,
即圆C的直角坐标方程为x2+y2-4y=0.
(2)由题意,得直线l的参数方程为
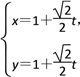 (t为参数).
(t为参数).
将该方程代入圆C的方程x2+y2-4y=0,
得![]() +
+![]() -4
-4![]() =0,
=0,
即t2=2,∴t1=![]() ,t2=-
,t2=-![]() .
.
即|PA|·|PB|=|t1t2|=2.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面![]() 列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 |
|
| |
不支持 |
|
| |
合计 |
(2)若对年龄在![]() ,
, ![]() 的被调查人中各随机选取两人进行调查,记选中的4人中不支持“生育二胎”人数为
的被调查人中各随机选取两人进行调查,记选中的4人中不支持“生育二胎”人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
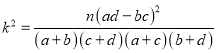 ,其中
,其中![]() .
.
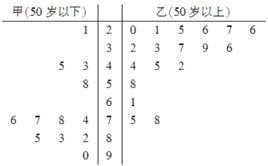
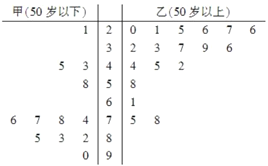
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
(1)根据以上数据完成下列![]() 的列联表;
的列联表;
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
主食蔬菜 | 主食肉类 | 合计 |
| |
50岁以下 | ||||
50岁以上 | ||||
合计 | ||||
参考公式:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
(1)根据以上数据完成下列![]() 的列联表;
的列联表;
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
主食蔬菜 | 主食肉类 | 合计 |
| |
50岁以下 | ||||
50岁以上 | ||||
合计 | ||||
参考公式: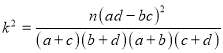
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |