题目内容
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
【答案】(Ⅰ)![]() ,
,![]() ,
,![]() 三类行业中每类行业的单位个数分别为60,60,80.(Ⅱ)
三类行业中每类行业的单位个数分别为60,60,80.(Ⅱ)![]()
【解析】
第一问利用分层抽样的概念直接计算即可;第二问是古典概率模型,先列出所有的基本事件,然后再找出3个单位都是“星级”环保单位或都是“非星级”环保单位所包含基本事件的个数,即可求出3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率。
(I)由题意,得抽取的![]() ,
,![]() ,
,![]() 三类行业单位个数之比为
三类行业单位个数之比为![]() .
.
由分层抽样的定义,有
![]() 类行业的单位个数为
类行业的单位个数为![]() ,
,
![]() 类行业的单位个数为
类行业的单位个数为![]() ,
,
![]() 类行业的单位个数为
类行业的单位个数为![]() ,
,
故该城区![]() ,
,![]() ,
,![]() 三类行业中每类行业的单位个数分别为60,60,80.
三类行业中每类行业的单位个数分别为60,60,80.
(Ⅱ)记选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位为事件![]() .
.
这3个单位的考核数据情形有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共20种.
,共20种.
这3个单位都是“星级”环保单位的考核数据情形有![]() ,
,![]() ,
,![]() ,
,![]() ,共4种,没有都是“非星级”环保单位的情形,
,共4种,没有都是“非星级”环保单位的情形,
故这3个单位都是“星级”环保单位或都是“非星级”环保单位的情形共4种,
故所求概率![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
附: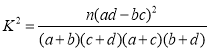 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究,全年级共有1350人,男女生比例为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() ,通过对被抽取学生的问卷调查,得到如下
,通过对被抽取学生的问卷调查,得到如下![]() 列联表:
列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(1)完成列联表,并判断能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(2)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界值表:![]()
| 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |