题目内容
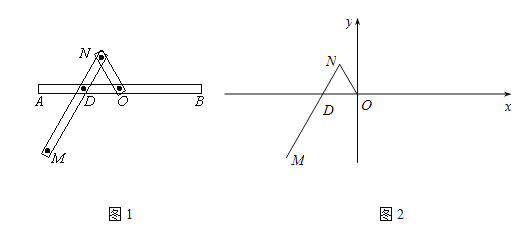
【题目】一种作图工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆
的中点,短杆![]() 可绕
可绕![]() 转动,长杆
转动,长杆![]() 通过
通过![]() 处铰链与
处铰链与![]() 连接,
连接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且![]() ,
,![]() .当栓子
.当栓子![]() 在滑槽AB内作往复运动时,带动
在滑槽AB内作往复运动时,带动![]() 绕
绕![]() 转动一周(
转动一周(![]() 不动时,
不动时,![]() 也不动),
也不动),![]() 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为![]() .以
.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(Ⅰ)求曲线C的方程;
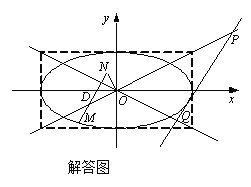
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线
总与曲线![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)存在最小值8.
;(Ⅱ)存在最小值8.
【解析】
(Ⅰ)设点![]() ,
,![]() ,依题意,
,依题意,
![]() ,且
,且![]() ,
,
所以![]() ,且
,且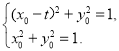
即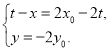 且
且![]()
由于当点![]() 不动时,点
不动时,点![]() 也不动,所以
也不动,所以![]() 不恒等于0,
不恒等于0,
于是![]() ,故
,故![]() ,代入
,代入![]() ,可得
,可得![]() ,
,
即所求的曲线![]() 的方程为
的方程为![]()
(Ⅱ)(1)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 为
为![]() 或
或![]() ,都有
,都有![]() .
.
(2)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() ,
,
由![]() 消去
消去![]() ,可得
,可得![]() .
.
因为直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,
有且只有一个公共点,
所以![]() ,即
,即![]() . ①
. ①
又由![]() 可得
可得![]() ;同理可得
;同理可得![]() .
.
由原点![]() 到直线
到直线![]() 的距离为
的距离为![]() 和
和![]() ,可得
,可得
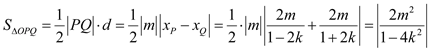 . ②
. ②
将①代入②得,![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
因![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
当且仅当![]() 时取等号.
时取等号.
所以当![]() 时,
时,![]() 的最小值为8.
的最小值为8.
综合(1)(2)可知,当直线![]() 与椭圆
与椭圆![]() 在四个顶点处相切时,
在四个顶点处相切时,![]() 的面积取得最小值8.
的面积取得最小值8.

练习册系列答案
相关题目