题目内容
【题目】已知数列![]() 是公差为正数的等差数列,数列
是公差为正数的等差数列,数列![]() 为等比数列,且
为等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 是由所有
是由所有![]() 的项,且
的项,且![]() 的项组成的数列,且原项数先后顺序保持不变,求数列
的项组成的数列,且原项数先后顺序保持不变,求数列![]() 的前2019项的和
的前2019项的和![]() ;
;
(3)对任意给定的![]() 是否存在
是否存在![]() 使
使![]() 成等差数列?若存在,用
成等差数列?若存在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组即可);若不存在,请说明理由.
(只要写出一组即可);若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)4105449;(3)当
;(2)4105449;(3)当![]() 时,不存在
时,不存在![]() ,
,
当![]() 时,存在
时,存在![]() ,
,![]() 满足要求
满足要求
【解析】
(1)设出公差![]() ,根据等差数列和等比数列的通项公式列方程求解即可;
,根据等差数列和等比数列的通项公式列方程求解即可;
(2)找出数列![]() 的前2019项中有多少项在数列
的前2019项中有多少项在数列![]() 中,在求和的过程中减去即可;
中,在求和的过程中减去即可;
(3)分类尝试,当![]() 时,发现不存在;当
时,发现不存在;当![]() 时,设
时,设![]() ,利用等差数列的通项公式,将
,利用等差数列的通项公式,将![]() 均用
均用![]() 表示出来,即可找出关系,得出结果.
表示出来,即可找出关系,得出结果.
解:(1)设数列![]() 的公差为
的公差为![]() ,
,![]()
则![]() ,
,
即![]() ,
,
![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以![]() ,即
,即![]() ,
,
又![]() ,
,
所以等比数列![]() 的公比
的公比![]() ,
,
所以![]() ,即
,即![]() ;
;
(2)![]() ,故数列
,故数列![]() 由数列
由数列![]() 的前2019+8项中减去数列
的前2019+8项中减去数列![]() 的前8项构成,
的前8项构成,
设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列 ![]() 的前
的前![]() 项和为
项和为![]()
![]() ;
;
(3)当![]() 时,若存在
时,若存在![]() 使
使![]() 成等差数列,
成等差数列,
则![]() ,
,
因为![]() ,所以
,所以![]() ,与数列
,与数列![]() 为正项数列相矛盾,
为正项数列相矛盾,
因此,当![]() 不存在;
不存在;
当![]() 时,设
时,设![]() ,
,
则![]() ,所以
,所以![]() ,
,
令![]() ,得
,得![]() 。
。
此时![]() ,
,
所以![]() ,
,
所以![]() ,
,
综上所述,当![]() 时,不存在
时,不存在![]() ,
,
当![]() 时,存在
时,存在![]() ,
,![]() 满足要求.
满足要求.

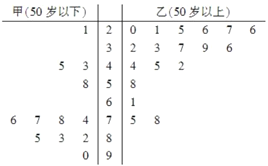
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
(1)根据以上数据完成下列![]() 的列联表;
的列联表;
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关,并写出简要分析.
主食蔬菜 | 主食肉类 | 合计 |
| |
50岁以下 | ||||
50岁以上 | ||||
合计 | ||||
参考公式: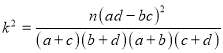
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究,全年级共有1350人,男女生比例为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() ,通过对被抽取学生的问卷调查,得到如下
,通过对被抽取学生的问卷调查,得到如下![]() 列联表:
列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(1)完成列联表,并判断能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(2)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界值表:![]()
| 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |