题目内容
如图,正方形ABCD内接于椭圆 =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.

(1)若正方形ABCD的边长为4,且与y轴交于E、F两点,正方形MNPQ的边长为2.
①求证:直线AM与△ABE的外接圆相切;
②求椭圆的标准方程;
(2)设椭圆的离心率为e,直线AM的斜率为k,求证:2e2-k是定值.
 =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
(1)若正方形ABCD的边长为4,且与y轴交于E、F两点,正方形MNPQ的边长为2.
①求证:直线AM与△ABE的外接圆相切;
②求椭圆的标准方程;
(2)设椭圆的离心率为e,直线AM的斜率为k,求证:2e2-k是定值.
(1)①见解析②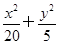 =1(2)见解析
=1(2)见解析
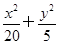 =1(2)见解析
=1(2)见解析(1)证明:①依题意:A(2,2),M(4,1),E(0,-2),∴ =(2,-1),
=(2,-1),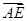 =(-2,-4),∴
=(-2,-4),∴ ·
·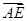 =0,∴AM⊥AE.
=0,∴AM⊥AE.
∵AE为Rt△ABE外接圆直径,∴直线AM与△ABE的外接圆相切.
②解:由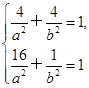 解得椭圆标准方程为
解得椭圆标准方程为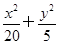 =1.
=1.
(2)证明:设正方形ABCD的边长为2s,正方形MNPQ的边长为2t,则A(s,s),M(s+2t,t),代入椭圆方程 =1,得
=1,得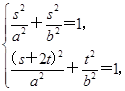 即
即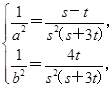
∴e2=1-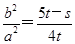 .∵k=
.∵k=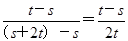 ,∴2e2-k=2为定值.
,∴2e2-k=2为定值.
 =(2,-1),
=(2,-1),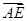 =(-2,-4),∴
=(-2,-4),∴ ·
·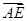 =0,∴AM⊥AE.
=0,∴AM⊥AE.∵AE为Rt△ABE外接圆直径,∴直线AM与△ABE的外接圆相切.
②解:由
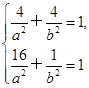 解得椭圆标准方程为
解得椭圆标准方程为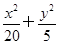 =1.
=1.(2)证明:设正方形ABCD的边长为2s,正方形MNPQ的边长为2t,则A(s,s),M(s+2t,t),代入椭圆方程
 =1,得
=1,得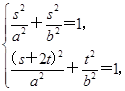 即
即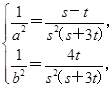
∴e2=1-
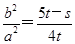 .∵k=
.∵k=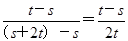 ,∴2e2-k=2为定值.
,∴2e2-k=2为定值.
练习册系列答案
相关题目
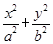 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为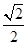 ,短轴的一个端点为M(0,1),直线l:y=kx-
,短轴的一个端点为M(0,1),直线l:y=kx-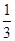 与椭圆相交于不同的两点A、B.
与椭圆相交于不同的两点A、B.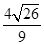 ,求k的值;
,求k的值; 和双曲线
和双曲线 的一个交点,
的一个交点,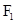 、
、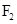 分别是它们的左右焦点.设椭圆离心率为
分别是它们的左右焦点.设椭圆离心率为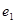 ,双曲线离心率为
,双曲线离心率为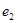 ,若
,若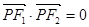 ,则
,则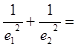 ( )
( )
 与双曲线
与双曲线 在交点处正交,则椭圆
在交点处正交,则椭圆

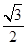

 =1有相同的焦点,直线y=
=1有相同的焦点,直线y= x为C的一条渐近线.求双曲线C的方程.
x为C的一条渐近线.求双曲线C的方程. =1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为 ,点M的横坐标为
,点M的横坐标为 .
.
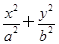 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.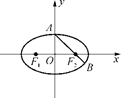
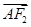 =2
=2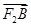 ,
,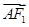 ·
·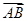 =
=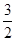 ,求椭圆的方程.
,求椭圆的方程. +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
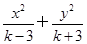 =1表示椭圆,则k的取值范围是________.
=1表示椭圆,则k的取值范围是________.