题目内容
已知椭圆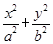 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为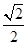 ,短轴的一个端点为M(0,1),直线l:y=kx-
,短轴的一个端点为M(0,1),直线l:y=kx-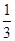 与椭圆相交于不同的两点A、B.
与椭圆相交于不同的两点A、B.
(1)若AB=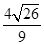 ,求k的值;
,求k的值;
(2)求证:不论k取何值,以AB为直径的圆恒过点M.
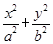 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为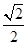 ,短轴的一个端点为M(0,1),直线l:y=kx-
,短轴的一个端点为M(0,1),直线l:y=kx-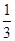 与椭圆相交于不同的两点A、B.
与椭圆相交于不同的两点A、B.(1)若AB=
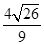 ,求k的值;
,求k的值;(2)求证:不论k取何值,以AB为直径的圆恒过点M.
(1)k=±1.(2)见解析
(1)解:由题意知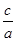 =
=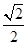 ,b=1.由a2=b2+c2可得c=b=1,a=
,b=1.由a2=b2+c2可得c=b=1,a= ,
,
∴椭圆的方程为 +y2=1.由
+y2=1.由 得(2k2+1)x2-
得(2k2+1)x2- kx-
kx- =0.
=0.
Δ= k2-4(2k2+1)×
k2-4(2k2+1)× =16k2+
=16k2+ >0恒成立,
>0恒成立,
设A(x1,y1),B(x2,y2),则x1+x2=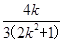 ,x1x2=-
,x1x2=- .
.
∴AB= ·|x1-x2|=
·|x1-x2|= ,化简得23k4-13k2-10=0,即(k2-1)(23k2+10)=0,解得k=±1.
,化简得23k4-13k2-10=0,即(k2-1)(23k2+10)=0,解得k=±1.
(2)证明:∵ =(x1,y1-1),
=(x1,y1-1), =(x2,y2-1),
=(x2,y2-1),
∴ =x1x2+(y1-1)(y2-1)=(1+k2)x1x2-
=x1x2+(y1-1)(y2-1)=(1+k2)x1x2- k(x1+x2)+
k(x1+x2)+ =-
=- -
- +
+ =0.∴不论k取何值,以AB为直径的圆恒过点M.
=0.∴不论k取何值,以AB为直径的圆恒过点M.
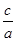 =
=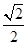 ,b=1.由a2=b2+c2可得c=b=1,a=
,b=1.由a2=b2+c2可得c=b=1,a= ,
,∴椭圆的方程为
 +y2=1.由
+y2=1.由 得(2k2+1)x2-
得(2k2+1)x2- kx-
kx- =0.
=0.Δ=
 k2-4(2k2+1)×
k2-4(2k2+1)× =16k2+
=16k2+ >0恒成立,
>0恒成立,设A(x1,y1),B(x2,y2),则x1+x2=
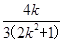 ,x1x2=-
,x1x2=- .
.∴AB=
 ·|x1-x2|=
·|x1-x2|= ,化简得23k4-13k2-10=0,即(k2-1)(23k2+10)=0,解得k=±1.
,化简得23k4-13k2-10=0,即(k2-1)(23k2+10)=0,解得k=±1.(2)证明:∵
 =(x1,y1-1),
=(x1,y1-1), =(x2,y2-1),
=(x2,y2-1),∴
 =x1x2+(y1-1)(y2-1)=(1+k2)x1x2-
=x1x2+(y1-1)(y2-1)=(1+k2)x1x2- k(x1+x2)+
k(x1+x2)+ =-
=- -
- +
+ =0.∴不论k取何值,以AB为直径的圆恒过点M.
=0.∴不论k取何值,以AB为直径的圆恒过点M.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
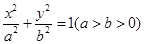 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线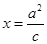 与x轴交于点B且与直线
与x轴交于点B且与直线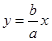 交于点C,点O为坐标原点,
交于点C,点O为坐标原点,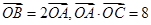 ,过点F的直线
,过点F的直线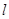 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.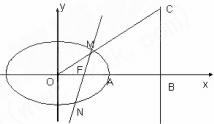
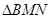 的面积的最大值.
的面积的最大值.  =1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
=1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切. =1;
=1; ,求椭圆E的方程;
,求椭圆E的方程; ·
· =0,试判断直线l与圆C的位置关系,并说明理由.
=0,试判断直线l与圆C的位置关系,并说明理由.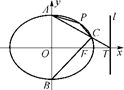
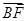 =3
=3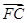 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为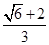 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标. =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
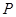 是椭圆
是椭圆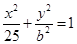 ,
,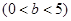 上除顶点外的一点,
上除顶点外的一点,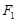 是椭圆的左焦点,若
是椭圆的左焦点,若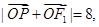 则点
则点
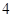


 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值. =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合. 的右焦点F2,且与椭圆E在第一象限的交点为M,与y轴交于点N,F1是椭圆E的左焦点,且|MN|=|MF1|,则椭圆E的方程为 .
的右焦点F2,且与椭圆E在第一象限的交点为M,与y轴交于点N,F1是椭圆E的左焦点,且|MN|=|MF1|,则椭圆E的方程为 .