题目内容
如图,已知椭圆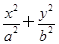 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
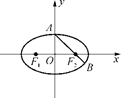
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若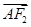 =2
=2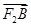 ,
,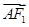 ·
·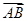 =
=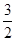 ,求椭圆的方程.
,求椭圆的方程.
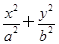 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若
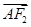 =2
=2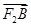 ,
,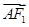 ·
·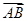 =
=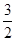 ,求椭圆的方程.
,求椭圆的方程.(1) (2)
(2) =1
=1
 (2)
(2) =1
=1(1)若∠F1AB=90°,则△AOF2为等腰直角三角形,所以有OA=OF2,即b=c.所以a= c,e=
c,e=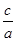 =
= .
.
(2)由题知A(0,b),F1(-c,0),F2(c,0),
其中,c= ,设B(x,y).
,设B(x,y).
由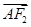 =2
=2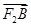 ,得(c,-b)=2(x-c,y),
,得(c,-b)=2(x-c,y),
解得x= ,y=-
,y=- ,即B
,即B .
.
将B点坐标代入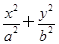 =1,得
=1,得 =1,即
=1,即 =1,解得a2=3c2.①
=1,解得a2=3c2.①
又由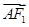 ·
·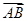 =(-c,-b)·
=(-c,-b)· ,得b2-c2=1,即有a2-2c2=1.②
,得b2-c2=1,即有a2-2c2=1.②
由①②解得c2=1,a2=3,从而有b2=2.
所以椭圆方程为 =1.
=1.
 c,e=
c,e=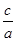 =
= .
.(2)由题知A(0,b),F1(-c,0),F2(c,0),
其中,c=
 ,设B(x,y).
,设B(x,y).由
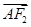 =2
=2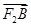 ,得(c,-b)=2(x-c,y),
,得(c,-b)=2(x-c,y),解得x=
 ,y=-
,y=- ,即B
,即B .
.将B点坐标代入
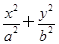 =1,得
=1,得 =1,即
=1,即 =1,解得a2=3c2.①
=1,解得a2=3c2.①又由
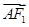 ·
· =(-c,-b)·
=(-c,-b)· ,得b2-c2=1,即有a2-2c2=1.②
,得b2-c2=1,即有a2-2c2=1.②由①②解得c2=1,a2=3,从而有b2=2.
所以椭圆方程为
 =1.
=1.
练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
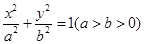 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线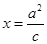 与x轴交于点B且与直线
与x轴交于点B且与直线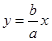 交于点C,点O为坐标原点,
交于点C,点O为坐标原点,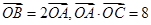 ,过点F的直线
,过点F的直线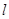 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.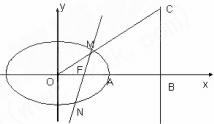
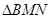 的面积的最大值.
的面积的最大值.  =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,F为椭圆的右焦点,M、N两点在椭圆C上,且
,F为椭圆的右焦点,M、N两点在椭圆C上,且 =λ
=λ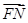 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0). ⊥
⊥ ;
; ·
· =
= ,求椭圆C的方程..
,求椭圆C的方程.. =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合. ,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点.
,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点. ,求椭圆的方程;
,求椭圆的方程; ·
· <7时,求椭圆离心率的取值范围.
<7时,求椭圆离心率的取值范围.
 的右焦点F2,且与椭圆E在第一象限的交点为M,与y轴交于点N,F1是椭圆E的左焦点,且|MN|=|MF1|,则椭圆E的方程为 .
的右焦点F2,且与椭圆E在第一象限的交点为M,与y轴交于点N,F1是椭圆E的左焦点,且|MN|=|MF1|,则椭圆E的方程为 . +
+ =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )


