题目内容
双曲线C与椭圆 =1有相同的焦点,直线y=
=1有相同的焦点,直线y= x为C的一条渐近线.求双曲线C的方程.
x为C的一条渐近线.求双曲线C的方程.
 =1有相同的焦点,直线y=
=1有相同的焦点,直线y= x为C的一条渐近线.求双曲线C的方程.
x为C的一条渐近线.求双曲线C的方程.x2- =1
=1
 =1
=1设双曲线的方程为 =1(a>0,b>0),
=1(a>0,b>0),
由椭圆方程 =1,求得两焦点为(-2,0)、(2,0),∴对于双曲线C:c=2.
=1,求得两焦点为(-2,0)、(2,0),∴对于双曲线C:c=2.
又y= x为双曲线C的一条渐近线,∴
x为双曲线C的一条渐近线,∴ =
= ,解得a2=1,b2=3.
,解得a2=1,b2=3.
∴双曲线C的方程为x2- =1.
=1.
 =1(a>0,b>0),
=1(a>0,b>0),由椭圆方程
 =1,求得两焦点为(-2,0)、(2,0),∴对于双曲线C:c=2.
=1,求得两焦点为(-2,0)、(2,0),∴对于双曲线C:c=2.又y=
 x为双曲线C的一条渐近线,∴
x为双曲线C的一条渐近线,∴ =
= ,解得a2=1,b2=3.
,解得a2=1,b2=3.∴双曲线C的方程为x2-
 =1.
=1.
练习册系列答案
相关题目
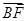 =3
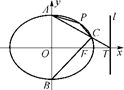
=3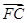 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为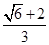 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标. 的焦距为2,且过点
的焦距为2,且过点 .
. ,
, ,过点
,过点 与椭圆C交于
与椭圆C交于 两点.
两点. 时,求
时,求 的长;
的长; 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
 +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点( ,
, ).
).
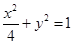 的焦点分别为
的焦点分别为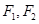 ,弦
,弦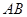 过点
过点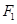 ,则
,则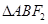 的周长为
的周长为


 =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合. ,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点.
,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点. ,求椭圆的方程;
,求椭圆的方程; ·
· <7时,求椭圆离心率的取值范围.
<7时,求椭圆离心率的取值范围.