题目内容
【题目】已知数列{an}是公差不为零的等差数列,a1=1,且a2 , a4 , a8成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:a1b1+a2b2+a3b3+…+anbn=2n+1 , n∈N* , 令cn= ![]() ,n∈N* , 求数列{cncn+1}的前n项和Sn .
,n∈N* , 求数列{cncn+1}的前n项和Sn .
【答案】
(1)解:设等差数列{an}的公差为d,
∵a1=1,且a2,a4,a8成等比数列.
∴ ![]() ,即
,即 ![]() ,
,
解得d=0(舍)或d=1,
∴数列{an}的通项公式为an=a1+(n﹣1)d=n,即an=n.
(2)解:由 ![]() ,
,
![]() (n≥2),
(n≥2),
两式相减得 ![]() ,即
,即 ![]() (n≥2),
(n≥2),
则 ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)利用等差数列与等比数列的通项公式即可得出;(2)利用递推式可得 ![]() (n≥2),再利用“裂项求和”即可得出.
(n≥2),再利用“裂项求和”即可得出.
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系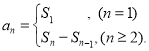 .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某同学用“五点法”画函数 ![]() 在区间[﹣
在区间[﹣ ![]() ,
, ![]() ]上的图象时,列表并填入了部分数据,如表:
]上的图象时,列表并填入了部分数据,如表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
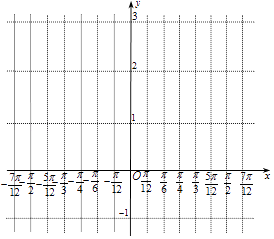
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象;
]上的图象;
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在 ![]() 时的值域.
时的值域.