题目内容
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件时,该服装厂获得的利润最大,最大利润是多少元? (服装厂售出一件服装的利润=实际出厂单价﹣成本)
【答案】
(1)解:当0<x≤100时,P=60,
当100<x≤500时,P=60﹣0.02(x﹣100)=62﹣ ![]() x,
x,
所以P=f(x)= 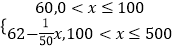 (x∈N)
(x∈N)
(2)解:设销售商的一次订购量为x件时,工厂获得的利润为L元,
则L=(P﹣40)x= 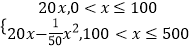 ,
,
此函数在[0,500]上是增函数,故当x=500时,函数取到最大值,
因此,当销售商一次订购了500件服装时,该厂获利的利润是6000元
【解析】(1)服装的实际出厂单价为P,应按x≤100和x>100两类分别计算,故函数P=f(x)应为分段函数;(2)由(1)可求出销售商一次订购了450件服装时的出厂价P,450(P﹣40)即为所求;也可列出当销售商一次订购x件服装时,该服装厂获得的利润函数,再求x=500时的函数值

练习册系列答案
相关题目