题目内容
10.设函数f(x)=x4-ax(a>0)的零点都在区间[0,5]上,则函数g(x)=$\frac{1}{x}$与函数h(x)=x3-a的图象的交点的横坐标为正整数时,实数a的所有取值中最大值为( )| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |
分析 由题意根据函数f(x)=x4-ax(a>0)的零点都在区间[0,5]上可得a的范围,然后然后再进行判断.
解答 解:∵函数f(x)=x4-ax(a>0)的零点都在区间[0,5]上,又f(x)=x4-ax=x(x3-a)
令f(x)=0,
∴x=0,或x=$\root{3}{a}$
∴$\root{3}{a}$≤5,
∴a≤125
由$\frac{1}{x}$=x3-a可得a=x3-$\frac{1}{x}$
令F(x)=x3-$\frac{1}{x}$(x≠0),则F′(x)=$3{x}^{2}+\frac{1}{{x}^{2}}$>0恒成立
∴F(x)在(0,+∞)上单调递增,在(-∞,0)上单调递增且F(1)=F(-1)=0
∵0<x3-$\frac{1}{x}$<125
当x=2,3,4,5时满足题意,
x=5时,a=125-$\frac{1}{5}$=$\frac{624}{5}$.
故选:C.
点评 此题考查函数的零点与方程根的关系,解题的关键是求出f(x)在区间[0,5]上的值域,是一道好题,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
18.已知集合A={0,1,2,3},集合B={x|x2≤4},则A∩B=( )
| A. | {3} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
5.房山区某高中为了推进新课程改革,满足学生全面发展的需求,决定从高一年级开始,在每周的周一、周三、周五的格外活动期间同时开设信息技术、美术素描和音乐欣赏辅导讲座,每位同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
(1)求音乐欣赏辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
| 信息技术 | 美术素描 | 音乐欣赏 | |
| 周一 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 周三 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 周五 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
19.“0<a<2”是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.若a>0,集合A={(x,y)|x≤3,x+y-4≤0,x-y+2a≥0},B={(x,y)||x-1|+|y-1|≤a}.若“点M(x,y)∈A”是“点M(x,y)∈B”的必要不充分条件,则实数a的取值范围是( )
| A. | (0,2) | B. | (1,3) | C. | (0,2] | D. | [1,3] |
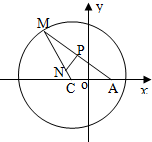 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在线段AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.求曲线E的方程.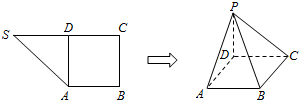
 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,