题目内容
设函数f(x)=sin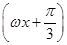 +sin
+sin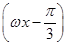 +
+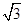 cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为
cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为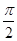 .
.
(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间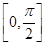 上的最大值和最小值.
上的最大值和最小值.
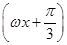 +sin
+sin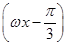 +
+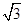 cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为
cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为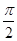 .
.(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间
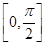 上的最大值和最小值.
上的最大值和最小值.(1)ω=2.(2)1
(1)f(x)=sin ωx+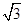 cos ωx=2sin
cos ωx=2sin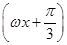 .
.
∵函数f(x)图象的两条相邻的对称轴间的距离为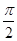 ,
,
∴T=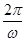 =π,∴ω=2.
=π,∴ω=2.
(2)由(1)得f(x)=2sin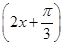 ,∴g(x)=2sin
,∴g(x)=2sin .
.
由x∈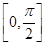 ,可得
,可得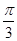 ≤x+
≤x+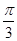 ≤
≤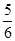 π,
π,
∴当x+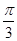 =
=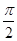 ,即x=
,即x=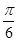 时,
时,
g(x)取得最大值g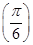 =2sin
=2sin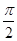 =2;
=2;
当x+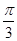 =
=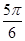 ,即x=
,即x=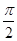 时,
时,
g(x)取得最小值g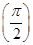 =2sin
=2sin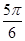 =1
=1
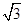 cos ωx=2sin
cos ωx=2sin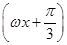 .
.∵函数f(x)图象的两条相邻的对称轴间的距离为
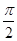 ,
,∴T=
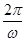 =π,∴ω=2.
=π,∴ω=2.(2)由(1)得f(x)=2sin
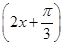 ,∴g(x)=2sin
,∴g(x)=2sin .
.由x∈
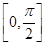 ,可得
,可得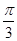 ≤x+
≤x+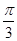 ≤
≤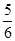 π,
π,∴当x+
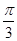 =
=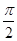 ,即x=
,即x=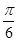 时,
时,g(x)取得最大值g
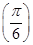 =2sin
=2sin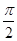 =2;
=2;当x+
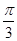 =
=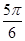 ,即x=
,即x=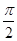 时,
时,g(x)取得最小值g
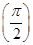 =2sin
=2sin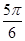 =1
=1
练习册系列答案
相关题目

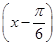 的图象,则φ=________.
的图象,则φ=________.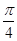 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值; ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值. (0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点. ·
· 的值;
的值; 的单调递增区间为 .
的单调递增区间为 . ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
 ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值. ,0]上为减函数的α值为( )
,0]上为减函数的α值为( )
 的部分图象如图,则φ的值为________.
的部分图象如图,则φ的值为________.