题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.

(1)求函数f(x)的解析式.
(2)当x∈[-6,- ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
 ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
(1)求函数f(x)的解析式.
(2)当x∈[-6,-
 ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.(1) f(x)=2sin( x+
x+ )
)
(2) 当 x=-
x=- ,即x=-
,即x=- 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值 ;
;
当 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2 .
.
 x+
x+ )
)(2) 当
 x=-
x=- ,即x=-
,即x=- 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值 ;
;当
 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2 .
.(1)由图象知A=2,T=8,
∵T= =8,∴ω=
=8,∴ω= .
.
又图象经过点(-1,0),∴2sin(- +φ)=0,
+φ)=0,
∴φ=kπ+ ,k∈Z,∵|φ|<
,k∈Z,∵|φ|< ,
,
∴φ= .∴f(x)=2sin(
.∴f(x)=2sin( x+
x+ ).
).
(2)y=f(x)+f(x+2)
=2sin( x+
x+ )+2sin(
)+2sin( x+
x+ +
+ )
)
=2 cos
cos x.
x.
∵x∈[-6,- ],∴-
],∴- ≤
≤ x≤-
x≤- .
.
∴当 x=-
x=- ,即x=-
,即x=- 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值 ;
;
当 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2 .
.
∵T=
 =8,∴ω=
=8,∴ω= .
.又图象经过点(-1,0),∴2sin(-
 +φ)=0,
+φ)=0,∴φ=kπ+
 ,k∈Z,∵|φ|<
,k∈Z,∵|φ|< ,
,∴φ=
 .∴f(x)=2sin(
.∴f(x)=2sin( x+
x+ ).
).(2)y=f(x)+f(x+2)
=2sin(
 x+
x+ )+2sin(
)+2sin( x+
x+ +
+ )
)=2
 cos
cos x.
x.∵x∈[-6,-
 ],∴-
],∴- ≤
≤ x≤-
x≤- .
.∴当
 x=-
x=- ,即x=-
,即x=- 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值 ;
;当
 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
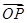 |=
|= ,
, =15,则此函数的解析式为________.
=15,则此函数的解析式为________.
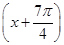 +cos
+cos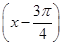 ,x∈R.
,x∈R.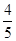 ,cos(β+α)=-
,cos(β+α)=-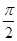 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0. ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )

 +2
+2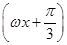 +sin
+sin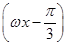 +
+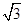 cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为
cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为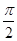 .
.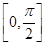 上的最大值和最小值.
上的最大值和最小值. ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )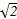 ]
] ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
 t+
t+ )
) t-
t- )
) )的一个单调区间是 ( )
)的一个单调区间是 ( ) ]
] ,
, ]
] ]
] sin 2x+2cos2x,则函数y=f(x)的单调递减区间为________.
sin 2x+2cos2x,则函数y=f(x)的单调递减区间为________.