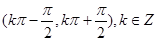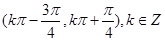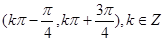题目内容
已知函数f(x)＝2sin
(0≤x≤5)，点A、B分别是函数y＝f(x)图象上的最高点和最低点．
(1)求点A、B的坐标以及
·
的值；
(2)设点A、B分别在角α、β的终边上，求tan(α－2β)的值．
(0≤x≤5)，点A、B分别是函数y＝f(x)图象上的最高点和最低点．(1)求点A、B的坐标以及
·的值；(2)设点A、B分别在角α、β的终边上，求tan(α－2β)的值．
（1）3（2）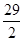
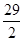
(1)∵0≤x≤5，∴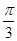
≤
≤
，
∴－
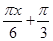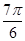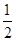≤sin≤1.
当＝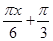
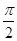，即x＝1时，sin＝1，f(x)取得最大值2；
当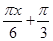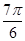＝，即x＝5时，sin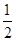＝－，f(x)取得最小值－1.
因此，点A、B的坐标分别是A(1,2)、B(5，－1)．
∴·＝1×5＋2×(－1)＝3.
(2)∵点A(1,2)、B(5，－1)分别在角α、β的终边上，
∴tan α＝2，tan β＝－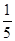
，
∵tan 2β＝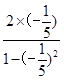
＝－
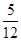，∴tan(α－2β)＝
.
≤≤，∴－
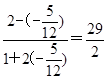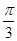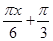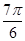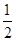≤sin≤1.当
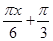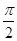＝，即x＝1时，sin＝1，f(x)取得最大值2；当
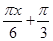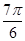＝，即x＝5时，sin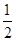＝－，f(x)取得最小值－1.因此，点A、B的坐标分别是A(1,2)、B(5，－1)．
∴
·＝1×5＋2×(－1)＝3.(2)∵点A(1,2)、B(5，－1)分别在角α、β的终边上，
∴tan α＝2，tan β＝－
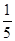，∵tan 2β＝
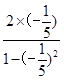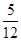＝－，∴tan(α－2β)＝.
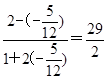练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
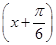，其中x∈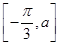
，若f(x)的值域是
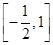，则a的取值范围是________．
在
上单调递减，则
可以是( )
，直线x＝
是其图象的一条对称轴，则符合条件的解析式为( )
＋2
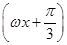＋sin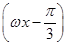
＋
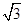cos ωx(其中ω＞0)，且函数f(x)的图象的两条相邻的对称轴间的距离为
.
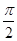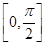上的最大值和最小值．
]上有零点,则实数m的取值范围为( )
]
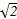)的一个单调区间是 ( )
]
,
]
]
的部分图像如图所示，当x∈0，
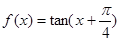单调增区间为（ ）
