题目内容
(本小题满分12分)
在直三棱柱中,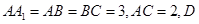 是
是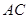 中点.
中点.
(1)求证: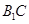 //平面
//平面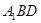 ;
;
(2)求点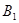 到平面
到平面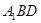 的距离;
的距离;
(3)求二面角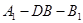 的余弦值.
的余弦值.
在直三棱柱中,
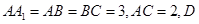 是
是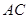 中点.
中点.
(1)求证:
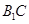 //平面
//平面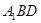 ;
;(2)求点
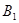 到平面
到平面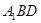 的距离;
的距离;(3)求二面角
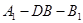 的余弦值.
的余弦值.(1)见解析;(2) 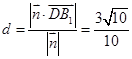 ;(3 )二面角的余弦值为
;(3 )二面角的余弦值为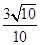 。
。
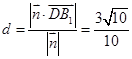 ;(3 )二面角的余弦值为
;(3 )二面角的余弦值为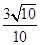 。
。本试题主要是考查了立体几何中线面平行的判定和线面垂直的判定以及二面角的求解的综合运用。
(1)利用线线平行得到线面平行的郑敏,这是一般的思路。
(2)合理的建立空间直角坐标系,然后根据斜向量在法向量上的投影,借助于向量的数量积的性质得到结论。
(3)根据上一问中的 法向量和法向量的夹角可以得到二面角平面角的求解。
解答:
(1)连结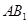 交
交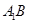 于
于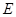 ,连结
,连结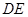 .
.
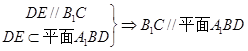 …….4分
…….4分
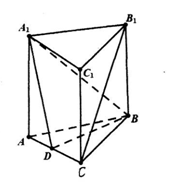
(2) 如图建立坐标系,
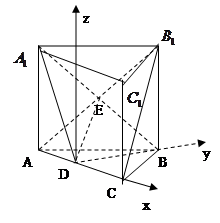
则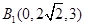 ,
,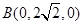 ,
,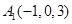
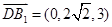 ,
,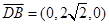
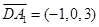
设平面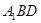 的法向量为
的法向量为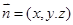 ,
,
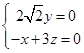 所以
所以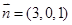 .
. 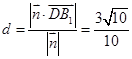 ……………..8分
……………..8分
(3 )平面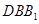 的法向量为
的法向量为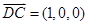 . 所以
. 所以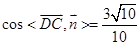
所以二面角的余弦值为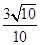 …………………………………………….12分
…………………………………………….12分
(1)利用线线平行得到线面平行的郑敏,这是一般的思路。
(2)合理的建立空间直角坐标系,然后根据斜向量在法向量上的投影,借助于向量的数量积的性质得到结论。
(3)根据上一问中的 法向量和法向量的夹角可以得到二面角平面角的求解。
解答:
(1)连结
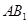 交
交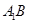 于
于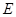 ,连结
,连结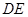 .
.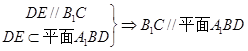 …….4分
…….4分(2) 如图建立坐标系,
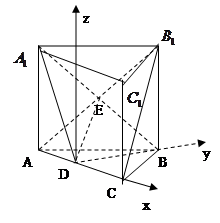
则
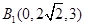 ,
,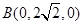 ,
,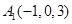
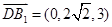 ,
,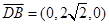
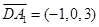
设平面
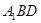 的法向量为
的法向量为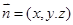 ,
,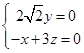 所以
所以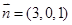 .
. 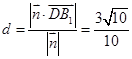 ……………..8分
……………..8分(3 )平面
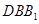 的法向量为
的法向量为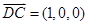 . 所以
. 所以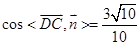
所以二面角的余弦值为
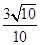 …………………………………………….12分
…………………………………………….12分
练习册系列答案
相关题目
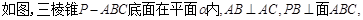
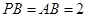 ,
,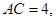
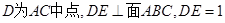 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.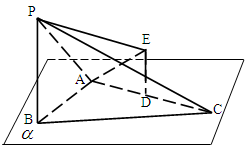
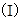 求证:BC//面APE;
求证:BC//面APE;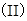 设F是
设F是 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小 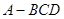 中,面
中,面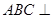 面
面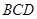 ,
,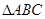 是正三角形,
是正三角形,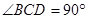 .
.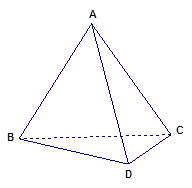
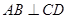 ;
;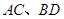 所成角的余弦值为
所成角的余弦值为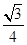 ,求二面角
,求二面角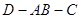 的大小;
的大小;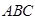
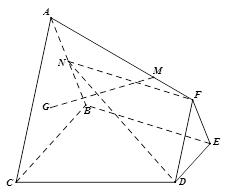
 平面
平面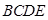 ,
, 与
与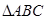 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,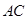 //
//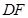 ,四边形
,四边形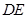 //
//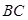 ,
,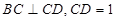 ,点
,点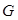 为
为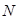 为
为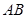 中点,
中点,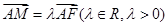 ,
,
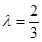 时,求证:
时,求证: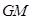 //平面
//平面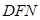
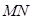 与
与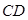 所成角为
所成角为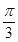 ,试求二面角
,试求二面角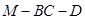 的余弦值.
的余弦值.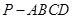 中,底面
中,底面 是矩形,
是矩形,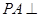 平面
平面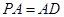 ,
,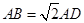 ,
,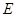 是线段
是线段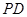 上的点,
上的点,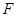 是线段
是线段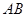 上的点,且
上的点,且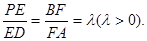

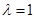 时,证明
时,证明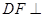 平面
平面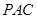 ;
;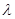 ,使异面直线
,使异面直线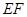 与
与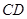 所成的角为
所成的角为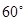 ?若存在,试求出
?若存在,试求出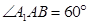 , M是A1B1的中点,
, M是A1B1的中点,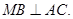
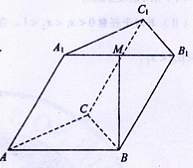
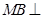 平面ABC;
平面ABC;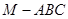 中,
中,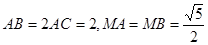 ,
,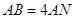 ,
,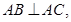 平面
平面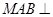 平面
平面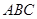 ,
,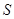 为
为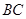 的中点.
的中点.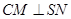 ;
;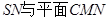 所成角的大小.
所成角的大小.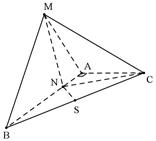
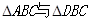 均是边长为2的等边三角形,且它们所在平面互相垂直,
均是边长为2的等边三角形,且它们所在平面互相垂直,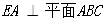 ,
,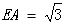 .
.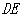 ||
|| 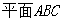
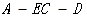 的余弦值。.
的余弦值。. 
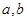 是不同的直线,
是不同的直线,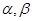 是不同的平面,则下列结论错误的是( )
是不同的平面,则下列结论错误的是( )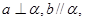 则
则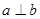
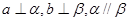 ,则
,则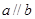
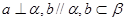 ,则
,则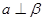
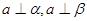 ,则
,则