题目内容
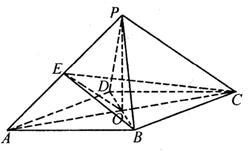
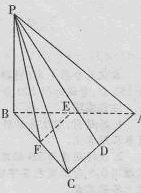
在四棱锥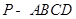 中,
中,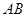 //
//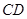 ,
,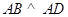 ,
, ,
,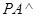 平面
平面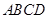 ,
,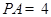 .
.
(Ⅰ)设平面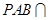 平面
平面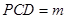 ,求证:
,求证: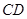 //
// ;
;
(Ⅱ)求证: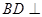 平面
平面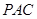 ;
;
(Ⅲ)设点 为线段
为线段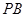 上一点,且直线
上一点,且直线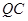 与平面
与平面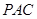 所成角的正弦值为
所成角的正弦值为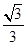 ,求
,求 的值.
的值.
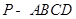 中,
中,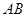 //
//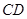 ,
,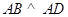 ,
, ,
,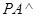 平面
平面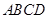 ,
,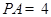 .
. (Ⅰ)设平面
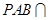 平面
平面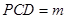 ,求证:
,求证: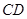 //
// ;
; (Ⅱ)求证:
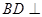 平面
平面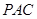 ;
;(Ⅲ)设点
 为线段
为线段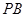 上一点,且直线
上一点,且直线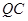 与平面
与平面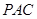 所成角的正弦值为
所成角的正弦值为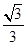 ,求
,求 的值.
的值.(Ⅰ)证明: 因为
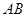 //
//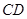 ,
,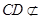 平面
平面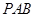 ,
,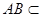 平面
平面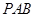 ,
,所以
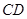 //平面
//平面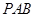 . ………………………………………2分
. ………………………………………2分因为
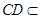 平面
平面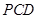 ,平面
,平面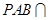 平面
平面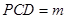 ,
,所以
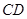 //
// . ………………………………………4分
. ………………………………………4分(Ⅱ)证明:因为
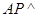 平面
平面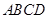 ,
,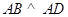 ,所以以
,所以以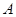 为坐标原点,
为坐标原点,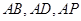 所在的直线分别为
所在的直线分别为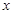 轴、
轴、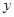 轴、
轴、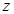 轴建立空间直角坐标系,
轴建立空间直角坐标系,则
 ,
,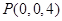 ,
,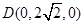 ,
,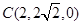 .
. ………………………………………5分
所以
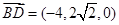 ,
,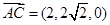 ,
,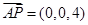 ,
,所以
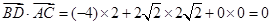 ,
,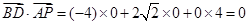 .
.所以
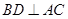 ,
,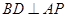 .
. 因为
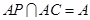 ,
,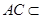 平面
平面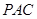 ,
,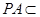 平面
平面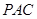 ,
,所以
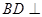 平面
平面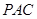 .
. ………………………………………9分
(Ⅲ)解:设
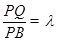 (其中
(其中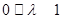 ),
),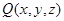 ,直线
,直线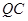 与平面
与平面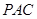 所成角为
所成角为
所以
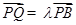 .
.所以
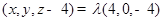 .
.所以
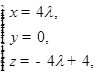 即
即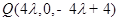 .
. 所以
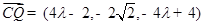 . ………………………………………11分
. ………………………………………11分由(Ⅱ)知平面
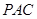 的一个法向量为
的一个法向量为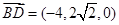 .
.………………………………………12分
因为
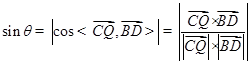 ,
,所以
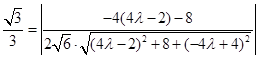 .
.解得
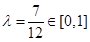 .
.所以
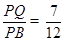 . ………………………………………14分
. ………………………………………14分略

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
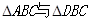 均是边长为2的等边三角形,且它们所在平面互相垂直,
均是边长为2的等边三角形,且它们所在平面互相垂直,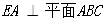 ,
,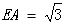 .
.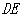 ||
|| 
 的余弦值。.
的余弦值。. 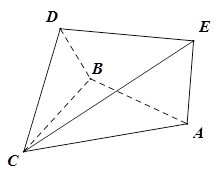
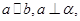 求证:
求证: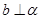 。
。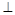 BD.
BD.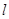 、
、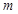 是两条不同的直线,
是两条不同的直线,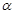 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是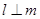 ,
,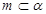 ,则
,则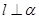
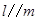 ,则
,则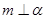
 ,
,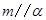 ,则
,则
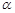 的一个充分条件是( )
的一个充分条件是( )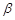 ,
,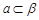 ,
,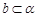 ,a∥b
,a∥b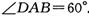 ,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.
,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.