题目内容
已知直三棱柱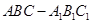 中,
中,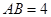 ,
,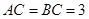 ,
,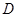 为
为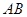 的中点。(Ⅰ)求点C到平面
的中点。(Ⅰ)求点C到平面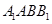 的距离;(Ⅱ)若
的距离;(Ⅱ)若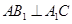 ,求二面角
,求二面角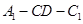 的平面角的余弦值。
的平面角的余弦值。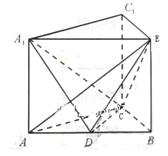
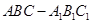 中,
中,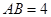 ,
,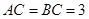 ,
,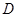 为
为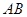 的中点。(Ⅰ)求点C到平面
的中点。(Ⅰ)求点C到平面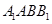 的距离;(Ⅱ)若
的距离;(Ⅱ)若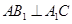 ,求二面角
,求二面角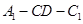 的平面角的余弦值。
的平面角的余弦值。
:(Ⅰ)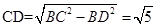 (Ⅱ)
(Ⅱ)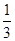
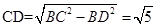 (Ⅱ)
(Ⅱ)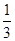
:(Ⅰ)因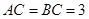 ,D为AB的中点,得
,D为AB的中点,得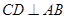 。又
。又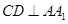 故
故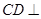 面
面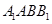 所以
所以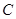 到平面
到平面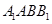 的距离为
的距离为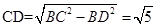
(Ⅱ):如答(19)图1,取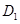 为
为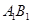 的中点,连接
的中点,连接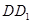 ,则
,则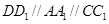 又由(Ⅰ)知
又由(Ⅰ)知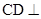 面
面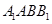 故
故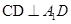 ,
,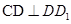 故
故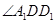 为所求的二面角
为所求的二面角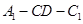 的平面角。
的平面角。
因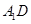 是
是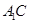 在面
在面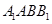 上的射影,又已知
上的射影,又已知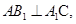 由三垂线定理的逆定理得
由三垂线定理的逆定理得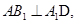 从而
从而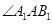 ,
,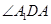 都与
都与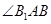 互余,因此
互余,因此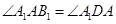 ,所以
,所以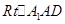 ≌
≌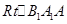 ,因此
,因此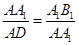 ,
,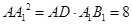 得
得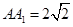
从而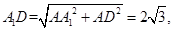 所以在
所以在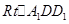 中,
中,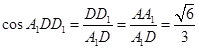
【考点定位】本小题主要考查立体几何的相关知识,具体涉及到线面垂直的关系、二面角的求法及空间向量在立体几何中的应用,解决此类问题的关键是熟悉几何体的结构特征,熟练进行线线垂直与线面垂直的转化,主要考查学生的空间想象能力与推理论证能力.本题可以利用空间向量来解题从而降低了题目的难度
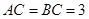 ,D为AB的中点,得
,D为AB的中点,得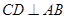 。又
。又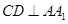 故
故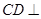 面
面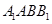 所以
所以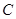 到平面
到平面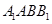 的距离为
的距离为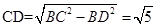
(Ⅱ):如答(19)图1,取
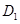 为
为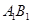 的中点,连接
的中点,连接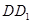 ,则
,则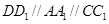 又由(Ⅰ)知
又由(Ⅰ)知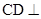 面
面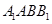 故
故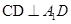 ,
,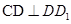 故
故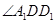 为所求的二面角
为所求的二面角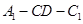 的平面角。
的平面角。因
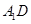 是
是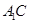 在面
在面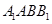 上的射影,又已知
上的射影,又已知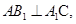 由三垂线定理的逆定理得
由三垂线定理的逆定理得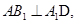 从而
从而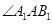 ,
,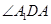 都与
都与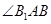 互余,因此
互余,因此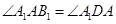 ,所以
,所以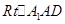 ≌
≌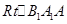 ,因此
,因此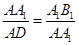 ,
,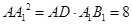 得
得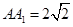
从而
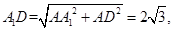 所以在
所以在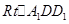 中,
中,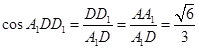
【考点定位】本小题主要考查立体几何的相关知识,具体涉及到线面垂直的关系、二面角的求法及空间向量在立体几何中的应用,解决此类问题的关键是熟悉几何体的结构特征,熟练进行线线垂直与线面垂直的转化,主要考查学生的空间想象能力与推理论证能力.本题可以利用空间向量来解题从而降低了题目的难度

练习册系列答案
相关题目
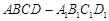 中,
中,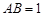 ,
,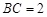 ,
,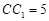 ,
,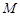 为棱
为棱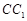 上一点.
上一点.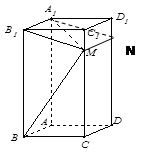
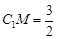 ,求异面直线
,求异面直线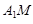 和
和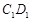 所成角的正切值;
所成角的正切值;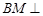 平面
平面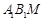 ?若存在,求出
?若存在,求出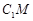 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.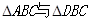 均是边长为2的等边三角形,且它们所在平面互相垂直,
均是边长为2的等边三角形,且它们所在平面互相垂直,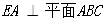 ,
,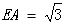 .
.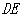 ||
|| 
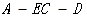 的余弦值。.
的余弦值。. 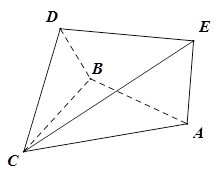
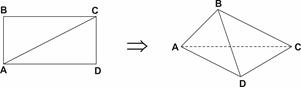
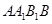 以边
以边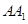 所在直线为轴旋转
所在直线为轴旋转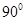 到正方形
到正方形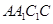 ,其中
,其中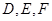 分别为
分别为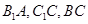 的中点.
的中点.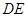 ∥平面
∥平面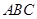 ;
;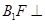 平面
平面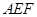 ;
;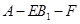 的大小.
的大小.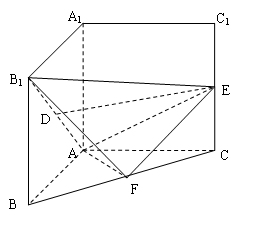
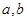 是不同的直线,
是不同的直线,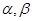 是不同的平面,则下列结论错误的是( )
是不同的平面,则下列结论错误的是( )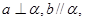 则
则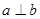
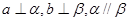 ,则
,则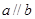
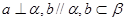 ,则
,则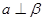
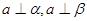 ,则
,则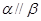
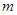 、
、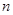 是两条不同的直线,
是两条不同的直线,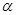 、
、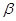 是两个不同的平面. 考察下列命题,其中真命题是
是两个不同的平面. 考察下列命题,其中真命题是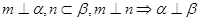
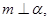
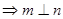
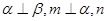 ∥
∥
 中,底面
中,底面 为矩形,平面
为矩形,平面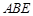 ,
,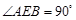 ,
,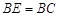 ,
,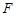 为
为 的中点,
的中点,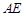 ∥平面
∥平面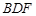 ;(2)平面
;(2)平面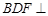 平面
平面 .
.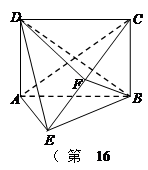
 BD.
BD.