题目内容
15.函数f(x)=$\sqrt{{3}^{x}-1}$+logx(4-3x)的定义域用区间表示为(0,1)∪(1,$\frac{4}{3}$).分析 根据函数成立的条件,即可得到结论.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{{3}^{x}-1≥0}\\{4-3x>0}\\{x>0且x≠1}\end{array}\right.$,
即$\left\{\begin{array}{l}{x≥0}\\{x<\frac{4}{3}}\\{x>0且x≠1}\end{array}\right.$,即0<x<$\frac{4}{3}$且x≠1,
即函数的定义域为(0,1)∪(1,$\frac{4}{3}$),
故答案为:(0,1)∪(1,$\frac{4}{3}$)
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
11.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第36颗珠子的颜色是 ( )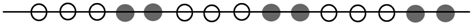
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |
5.已知点P是抛物线y2=2x上的动点,点P到准线的距离为d,且点P在y轴上的射影是M,点A($\frac{7}{2}$,4),则|PA|+|PM|的最小值是( )
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |