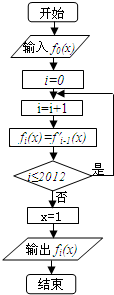
题目内容
16.设f(x)=ex(ax2+x+1)(a>0),试判断f(x)的单调性.分析 求导数,分类讨论,利用导数的正负,可讨论该函数的单调性.
解答 解:f′(x)=ex[ax2+(2a+1)x+2]=ex(ax+1)(x+2),
①0<a<$\frac{1}{2}$时,令f′(x)>0,解得:x>-2或x<-$\frac{1}{a}$,
令f′(x)<0,解得:-$\frac{1}{a}$<x<-2,
∴函数f(x)在(-∞,-$\frac{1}{a}$),(-2,+∞)递增,在(-$\frac{1}{a}$,-2)递减;
②a=$\frac{1}{2}$时,f′(x)≥0,f(x)在R上递增;
③a>$\frac{1}{2}$时,令f′(x)>0,解得:x>-$\frac{1}{a}$或x<-2,
令f′(x)<0,解得:-2<x<-$\frac{1}{a}$,
∴函数f(x)在(-∞,-2),(-$\frac{1}{a}$,+∞)递增,在(-2,-$\frac{1}{a}$)递减.
点评 本题以函数为载体,考查函数的单调性,做题时要注意对a进行讨论,最后得出函数的单调区间.

练习册系列答案
相关题目
4.已知点F(c,0)(c>0)是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,F关于直线y=$\frac{\sqrt{3}}{3}$x的对称点A 也在椭圆上,则该椭圆的离心率是( )
| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | -$\sqrt{3}$+2 |
11.在等差数列{an}中,an>0,且前10项和S10=30,则a5a6的最大值是( )
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
1.设a∈R,则“a>1”是“$\frac{1-{a}^{2}}{a}$<1-a”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
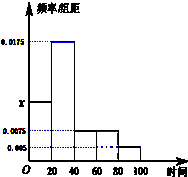 某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]
某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100] 如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期的图象.
如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期的图象.