题目内容
7.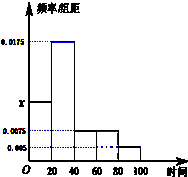 某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]
某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100](1)求直方图中的x的值;
(2)如果上学所需时间不少于1小时的学生可以申请乘校车,请计算400名新生中有多少名学生可以申请乘校车上学.
分析 (1)根据频率分布直方图的小矩形的面积和为1,求得x值;
(2)利用频率分布直方图先求上学所需时间不少于1小时的学生的频率,再利用频率乘以总体个数可得400名新生中有多少名学生可以申请乘校车上学.
解答 解:(1)由(x+0.005+0.0075×2+0.0175)×20=1,
解得x=0.0125;
(2)上学所需时间不少于1小时的学生的频率为:(0.005+0.0075)×20=0.25,
估计学校400名新生中有:400×0.25=100,
答:估计学校400名新生中有100名学生申请乘校车上学.
点评 本题考查了频率分布直方图,读懂频率分布直方图的数据含义是关键.

练习册系列答案
相关题目
17.由于工业化城镇化的推进,大气污染日益加重,空气质量逐步恶化,雾霾天气频率增大,大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如下列联表:问有多大的把握认为是否患心脏病与性别有关.答( )
(参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 患心脏病 | 不患心脏病 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 95% | B. | 99% | C. | 99.5% | D. | 99.9% |
19.调查某医院某段时间内婴儿出生的时间与性别的关系,得到部分数据如表:
你认为婴儿的性别与出生时间有关系的把握为( )
| 晚上 | 白天 | 合计 | |
| 男婴 | ? | 31 | 55 |
| 女婴 | 8 | ? | 34 |
| 合计 | 32 | 57 | 89 |
| A. | 80% | B. | 90% | C. | 95% | D. | 不能确定 |