题目内容
5. 如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期的图象.
如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期的图象.(Ⅰ)求函数f(x)的表达式;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)设0<α<π,若方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
分析 (Ⅰ)根据三角函数图象确定A,ω和φ的值即可求函数f(x)的表达式;
(Ⅱ)根据三角函数的单调性即可求函数f(x)的单调区间;
(Ⅲ)分别作出f(x)和y=m的图象,利用数形结合进行求解即可.
解答 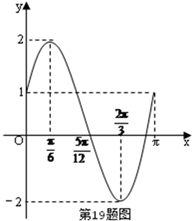 解:(Ⅰ)显然A=2,…(1分)
解:(Ⅰ)显然A=2,…(1分)
又图象过(0,1)点,∴f(0)=1,
∴$sinϕ=\frac{1}{2}$,∵$|ϕ|<\frac{π}{2}$,∴$ϕ=\frac{π}{6}$;
…(2分)
由图象结合“五点法”可知,$(\frac{11π}{12}{,^{\;}}0)$对应函数y=sinx图象的点(2π,0),
∴$ω×\frac{11π}{12}+\frac{π}{6}=2π$,ω=2.…(4分)
所以所求的函数的解析式为:$f(x)=2sin(2x+\frac{π}{6})$.…(5分)
(Ⅱ)当$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2},(k∈z)$时,函数$f(x)=2sin(2x+\frac{π}{6})$
单调递增,即$2kπ-\frac{2π}{3}≤2x≤2kπ+\frac{π}{3},(k∈z)$.…(7分)
解得$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}(k∈z)$.…(8分)
故函数$f(x)=2sin(2x+\frac{π}{6})$单调递增区间为$[kπ-\frac{π}{3},kπ+\frac{π}{6}](k∈z)$.…(9分)
(Ⅲ)如图所示,在同一坐标系中画出$y=2sin(2x+\frac{π}{6})$和y=m(m∈R) 的图象,
由图可知,当-2<m<1或1<m<2时,
直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根.…(10分)
∴m的取值范围为:-2<m<1或1<m<2;…(12分)
当-2<m<1时,两根和为$\frac{π}{3}$;当1<m<2时,两根和为$\frac{4π}{3}$.…(14分)
点评 本题主要考查三角函数的图象和性质,根据图象确定函数的解析式是解决本题的关键.要求熟练掌握三角函数的图象和性质.
