题目内容
8．正四棱台的上、下底面边长分别为2、4，侧棱长为4，求正四棱台的高和斜高．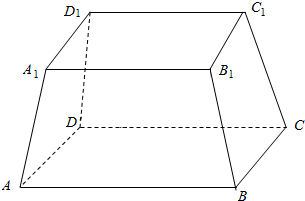
分析 取上底A1B1C1D1的中心O1和下底ABCD的中心O，连结OO1，过O1作O1F⊥A1B1，交A1B1于F，过O作OE⊥AB，交AB于E，过F作FN⊥OE，交OE于N，正四棱台的斜高B1K，正四棱台的高OO1=FN，由此能求出正四棱台的高和斜高．
解答 
解：取上底A1B1C1D1的中心O1和下底ABCD的中心O，连结OO1，
过O1作O1F⊥A1B1，交A1B1于F，过O作OE⊥AB，交AB于E，
过F作FN⊥OE，交OE于N，
正四棱台的斜高B1K=EF=$\sqrt{B{B}^{2}-（\frac{AB-{A}_{1}{B}_{1}}{2}）^{2}}$=$\sqrt{16-1}$=$\sqrt{15}$．
则正四棱台的高OO1=FN=$\sqrt{E{F}^{2}-（OE-{O}_{1}F）^{2}}$=$\sqrt{15-（4-2）^{2}}$=$\sqrt{11}$．
∴正四棱台的高是$\sqrt{11}$，斜高是$\sqrt{15}$．
点评 本题考查正四棱台的高和斜高的求法，是基础题，解题时要认真审题，注意空间思维能力和下四棱台的结构特征的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．函数f（x）对任意a，b∈R，有f（a+b）=f（a）+f（b）-1，且当x＞0时，f（x）＞1．
（Ⅰ）求证：f（x）是R 上的增函数；
（Ⅱ）若f（-4）=5，解不等式f（3m2-m-3）＜2．
（Ⅰ）求证：f（x）是R 上的增函数；
（Ⅱ）若f（-4）=5，解不等式f（3m2-m-3）＜2．
16．若6＜a＜10，$\frac{a}{2}$≤b≤2a，c=a+b，那么c的取值范围是（ ）
| A． | 9≤c≤18 | B． | 15＜c＜30 | C． | 9≤c≤30 | D． | 9＜c＜30 |
3．
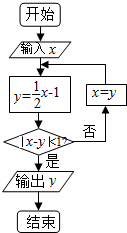执行如图所示的程序框图，若输入x的值为4，则输出的结果是（ ）
执行如图所示的程序框图，若输入x的值为4，则输出的结果是（ ）| A． | 1 | B． | $-\frac{1}{2}$ | C． | $-\frac{5}{4}$ | D． | $-\frac{13}{8}$ |
从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图），