题目内容
15.求下列函数的奇偶性:(1)f(x)=3x4-5x2+6;
(2)f(x)=x-2.
分析 根据函数奇偶性的定义,可判断出给定两个函数的奇偶性.
解答 解:(1)∵f(x)=3x4-5x2+6,
∴f(-x)=3(-x)4-5(-x)2+6=3x4-5x2+6=f(x);
∴f(x)=3x4-5x2+6为偶函数;
(2)∵f(x)=x-2,
∴f(-x)=-x-2,
f(-x)=f(x),f(-x)=-f(x)均不恒成立,
∴f(x)=x-2为非奇非偶函数.
点评 本题考查的知识点是函数奇偶性的定义和性质,难度不大,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
3.在首项为负数的等差数列{an}中,若a10+a11+a12=0,则当数列{an}的前n项和Sn取最小值时,n等于.
| A. | 10 | B. | 10或11 | C. | 11 | D. | 9或10 |
7.若f(x)=x+$\frac{1}{x}$,则下列式子中正确的是( )
| A. | f(-1)=0 | B. | f(0)=0 | C. | f(-x)=f(x) | D. | f($\frac{1}{x}$)=f(x) |
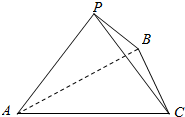 如图,三棱锥P-ABC的底面是边长为2的等边三角形.若PA=PB=$\sqrt{2}$.二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$.
如图,三棱锥P-ABC的底面是边长为2的等边三角形.若PA=PB=$\sqrt{2}$.二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$.