题目内容
18．下列函数中，在区间（0，+∞）上是增函数的是④．①y=-x2②y=$\frac{1}{x}$③y=（$\frac{1}{2}$）x④y=log2x．
分析 根据二次函数、反比例函数、指数函数、对数函数的单调性进行判断即可．
解答 解：①y=-x2在区间（0，+∞）上是减函数；
②y=$\frac{1}{x}$在区间（0，+∞）上是减函数；
③y=（$\frac{1}{2}$）x在区间（0，+∞）上是减函数；
④y=log2x在区间（0，+∞）上是增函数，
故答案为：④．
点评 本题考查二次函数、反比例函数、指数函数、对数函数的单调性，属于基础题．
练习册系列答案
相关题目
9．若实数x，y满足$\left\{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥1}\end{array}\right.$，则Z=2x+y-1的最大值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
6．函数f（x）=ax（a＞0且a≠1）在区间[1，2]上的最大值比最小值大$\frac{a}{4}$，则实数a的值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{4}或\frac{5}{4}$ | D． | $\frac{3}{4}或\frac{5}{4}$ |
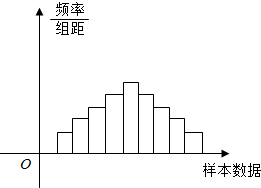在样本的频率分布直方图中，共有9个小长方形，若第一个长方形的面积为0.04，前五个与后五个长方形的面积分别成等差数列且公差是互为相反数，若样本容量为800，则中间一组（即第五组）的频数为160．
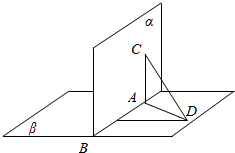已知A，B，是直二面角α-l-β的棱上两点，线段AC?α，线段BD?β，且AC⊥l，BD⊥l，AC=12，AB=4，BD=3，求线段CD的长．