题目内容
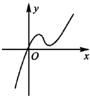
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若正数a,b满足f(2a+b)<1,则
的取值范围是( )
| a+2 |
| b+2 |
A.(
| B.(-∞,
| C.(
| D.(-∞,3) |

由图可知,当x>0时,导函数f'(x)>0,原函数单调递增
∵两正数a,b满足f(2a+b)<1,
∴0<2a+b<4,∴b<4-2a,0<a<2
∴
<
=
=-2+
∵0<a<2,∴
<-2+
<3,
从而
<
<2
故选A.
∵两正数a,b满足f(2a+b)<1,
∴0<2a+b<4,∴b<4-2a,0<a<2
∴
| b+2 |
| a+2 |
| 4-2a+2 |
| a+2 |
| 10-(2a+4) |
| a+2 |
| 10 |
| a+2 |
∵0<a<2,∴
| 1 |
| 2 |
| 10 |
| a+2 |
从而
| 1 |
| 3 |
| a+2 |
| b+2 |
故选A.

练习册系列答案
相关题目
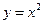 (
(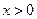 )与函数
)与函数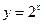 的图像所围成的封闭区域的面积.
的图像所围成的封闭区域的面积.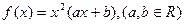 在
在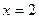 时有极值,其图象在点
时有极值,其图象在点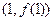 处的切线与直线
处的切线与直线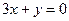 平行.(1)求
平行.(1)求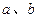 的值和函数
的值和函数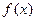 的单调区间;(2)若当
的单调区间;(2)若当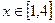 时,恒有
时,恒有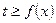 ,试确定
,试确定 的取值范围.
的取值范围.