作出函数y=x2-4|x|-5的图象.并写出函数的单调区间．题目和参考答案——青夏教育精英家教网——

题目内容

18．作出函数y=x²-4|x|-5的图象，并写出函数的单调区间．

分析作函数y=x²-4|x|-5的图象，从而写出函数的单调区间．

解答解：作函数y=x²-4|x|-5的图象如下，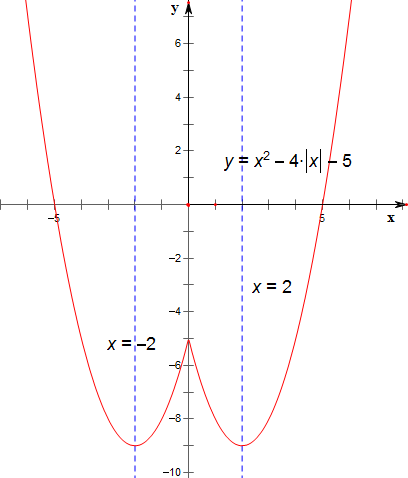

结合图象可知，
其单调减区间为（-∞，-2），（0，2）；
单调增区间为（2，+∞），（-2，0）．

点评本题考查了函数的图象的作法及应用．

练习册系列答案

期末闯关全程特训卷系列答案

小学期末冲刺100分系列答案

新编单元测试AB卷系列答案

期末夺冠满分测评卷系列答案

创新考王完全试卷系列答案

期末复习检测系列答案

超能学典单元期中期末专题冲刺100分系列答案

期末100分冲刺卷系列答案

黄冈360度定制密卷系列答案

聚能闯关期末复习冲刺卷系列答案

相关题目

1．已知一次函数y=f（x），且f{f[f（x）]}=$\frac{27}{8}$x+$\frac{19}{2}$，求y=f（x）的表达式．

9．C₃²+C₄²+C₅²+…+C₁₉²=1139．

6．已知函数f（x）=$\sqrt{3}sinωxcosωx+{cos^2}ωx-\frac{3}{2}$（ω＞0），其最小正周期为$\frac{π}{2}$．
（1）求f（x）的解析式；
（2）将函数f（x）的图象向右平移$\frac{π}{8}$个单位，再将图象上个点横坐标伸长到原来的2倍（纵坐标不变），得到函数y=g（x）的图象，若关于x的方程g（x）+k=0，在区间$[{\left.{0，\frac{π}{2}}]}$上有且只有两个实数解，求实数k的取值范围．
（3）若不等式$|{f（x）-m}|＜1在x∈[{\left.{0，\frac{π}{4}}]}$上恒成立，求实数m的取值范围．

13．在公比为2的等比数列{a_n}中，a₃=12，则a₅=48．

3．设向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ，$\overrightarrow{a}$=（2，1），$\overrightarrow{a}$+2$\overrightarrow{b}$=（4，5），则sinθ=$\frac{3}{5}$．

10．作五边形ABCDE，求作下列各题中的和向量：
（1）$\overrightarrow{AB}$+$\overrightarrow{BC}$；
（2）$\overrightarrow{AB}$+$\overrightarrow{ED}$+$\overrightarrow{DB}$+$\overrightarrow{BE}$．

7．设f（x）、g（x）分别是定义在R上的奇函数和偶函数．当x＜0时，f′（x）g（x）-f（x）g′（x）＞0且g（-3）=0．则不等式f（x）g（x）＜0的解集是（　　）

（-∞，-3）∪（0，3）

（-3，0）∪（0，3）

（-∞，-3）∪（3，+∞）

（-3，0）∪（3，+∞）

8．已知向量$\overrightarrow{a}$=（0，2$\sqrt{3}$），b=（1，$\sqrt{3}$），则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为（　　）