题目内容
8.已知向量$\overrightarrow{a}$=(0,2$\sqrt{3}$),b=(1,$\sqrt{3}$),则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )| A. | 3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -3 |
分析 由两向量的坐标求出两向量夹角的余弦值,代入投影公式得答案.
解答 解:由$\overrightarrow{a}=(0,2\sqrt{3})$,$\overrightarrow{b}=(1,\sqrt{3})$,得
cos$<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}=\frac{\sqrt{3}}{2}$,
∴向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>=2\sqrt{3}×\frac{\sqrt{3}}{2}=3$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影的概念,是基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
3.不等式$\sqrt{a^2-x^2}$<x+a(a>0)的解集是( )
| A. | {x|-$\frac{a}{2}$<x<a} | B. | {x|x>0或x$<-\frac{3}{5}$a} | ||
| C. | {x|-a≤x≤-$\frac{3}{5}$a或0≤x<a} | D. | {x|0<x≤a} |
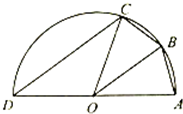 如图所示,AD是半径为5的半圆O的直径,B,C是半圆O上的两点,cos∠AOB=$\frac{4}{5}$,AB=BC,
如图所示,AD是半径为5的半圆O的直径,B,C是半圆O上的两点,cos∠AOB=$\frac{4}{5}$,AB=BC,