题目内容
20.在△ABC中,角A、B、C所对的边分别为a、b、c,若acosB+bcosA=csinC,则∠C=$\frac{π}{2}$.分析 由正弦定理把已知的等式化边为角,结合两角和的正弦化简,求出sinC,进一步求得∠C.
解答 解:由acosB+bcosA=csinC,结合正弦定理可得:sinAcosB+sinBcosA=sin2C,
∴sin(B+A)=sin2C,即sinC(sinC-1)=0,
在△ABC中,∵sinC≠0,∴sinC=1,
又0<C<π,∴∠C=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查正弦定理的应用,考查了两角和与差的三角函数,是中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
15.已知某天城市A下雨的概率为0.5,城市S下雨的概率为0.4,两城市同时下雨的概率为0,则两城市都没有下雨的概率为( )
| A. | 0.2 | B. | 0.5 | C. | 0.9 | D. | 0.1 |
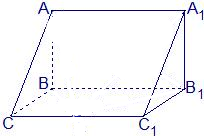 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,BC=1,∠BCC1=$\frac{π}{3}$,且异面直线A1C于B1C1所成角的大小为arccos$\frac{\sqrt{10}}{5}$,求:
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,BC=1,∠BCC1=$\frac{π}{3}$,且异面直线A1C于B1C1所成角的大小为arccos$\frac{\sqrt{10}}{5}$,求: