题目内容
(本小题满分13分)如图所示,直线l与抛物线y2=x交于A(x1,y1),B(x2,y2)两点,与x轴交于点M,且y1y2=-1,

(Ⅰ)求证:点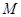 的坐标为
的坐标为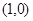 ;
;
(Ⅱ)求证:OA⊥OB;
(Ⅲ)求△AOB面积的最小值。

(Ⅰ)求证:点
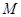 的坐标为
的坐标为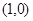 ;
;(Ⅱ)求证:OA⊥OB;
(Ⅲ)求△AOB面积的最小值。
(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)1
试题分析:(Ⅰ)设M(x0,0),直线l方程为x=my+x0代入y2=x得
y2-my-x0=0,y1。y2是此方程的两根
∴ x0=-y1y2=1 ① 即M点坐标是(1,0) (4分)
证明:(Ⅱ)∵ y1y2=-1 ∴ x1x2+y1y2=y1y2(y1y2+1)=0,
∴ OA⊥OB (8分)
(Ⅲ)由方程①得y1+y2=m,y1y2=-1,又|OM|=x0=1,
 ,
,∴ 当m=0时,S△AOB取最小值1。 (13分)
点评:直线与抛物线位置关系常联立方程,利用韦达定理求解

练习册系列答案
相关题目
 .过点P且与抛物线E交于A(xl,y1)、B( x2,y2)两点,直线
.过点P且与抛物线E交于A(xl,y1)、B( x2,y2)两点,直线 过点P且与抛物线E交于C(x3, y3)、D(x4,y4)两点.过点P作x轴的垂线,与线段AC和BD分别交于点M、N.
过点P且与抛物线E交于C(x3, y3)、D(x4,y4)两点.过点P作x轴的垂线,与线段AC和BD分别交于点M、N.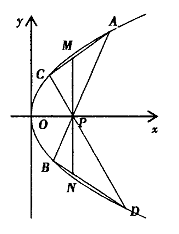
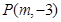 到焦点的距离等于5,
到焦点的距离等于5,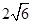
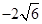

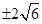
 ,
, 是抛物线
是抛物线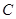 的焦点,过点
的焦点,过点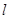 与
与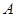 、
、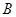 两点,
两点,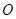 为坐标原点.
为坐标原点.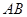 为直径的圆的方程;
为直径的圆的方程;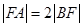 ,求直线
,求直线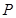 是抛物线
是抛物线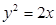 上的动点,
上的动点,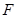 是抛物线的焦点,若点
是抛物线的焦点,若点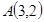 ,则
,则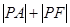 的最小值是 .
的最小值是 .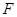 为抛物线
为抛物线 的焦点,
的焦点,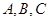 为抛物线上三点.
为抛物线上三点.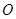 为坐标原点,若
为坐标原点,若 的重心,
的重心, 的面积分别为
的面积分别为 3,则
3,则 +
+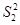 +
+ 的值为: ( )
的值为: ( ) 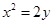 的焦点到准线的距离为( )
的焦点到准线的距离为( )
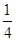
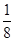
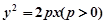 ,过其焦点且斜率为1的
,过其焦点且斜率为1的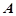 、
、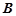 两点,若线段
两点,若线段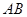 的中点的纵
的中点的纵