题目内容
(本小题12分)
给定抛物线 ,
,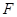 是抛物线
是抛物线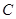 的焦点,过点
的焦点,过点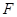 的直线
的直线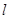 与
与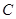 相交于
相交于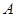 、
、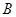 两点,
两点,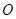 为坐标原点.
为坐标原点.
(Ⅰ)设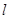 的斜率为1,求以
的斜率为1,求以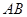 为直径的圆的方程;
为直径的圆的方程;
(Ⅱ)设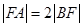 ,求直线
,求直线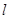 的方程.
的方程.
给定抛物线
 ,
,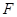 是抛物线
是抛物线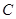 的焦点,过点
的焦点,过点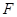 的直线
的直线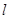 与
与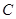 相交于
相交于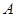 、
、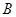 两点,
两点,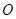 为坐标原点.
为坐标原点.(Ⅰ)设
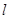 的斜率为1,求以
的斜率为1,求以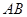 为直径的圆的方程;
为直径的圆的方程;(Ⅱ)设
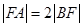 ,求直线
,求直线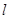 的方程.
的方程.(Ⅰ)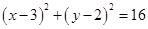 (Ⅱ)
(Ⅱ)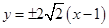
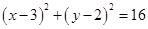 (Ⅱ)
(Ⅱ)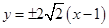
试题分析:(Ⅰ)解:
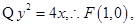 又
又 直线
直线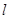 的斜率为1,
的斜率为1,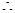 直线
直线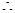
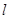 的方程为:
的方程为: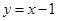 ,代入
,代入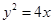 ,得:
,得: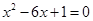 ,
,由根与系数的关系得:
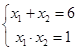 ,易得
,易得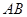 中点即圆心的坐标为
中点即圆心的坐标为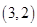 ,
,又
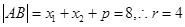 ,
, 所求的圆的方程为:
所求的圆的方程为: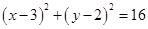 . ……4分
. ……4分(Ⅱ)
 而
而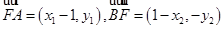 ,
, ,
, 直线
直线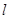 的斜率存在,
的斜率存在,设直线
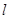 的斜率为
的斜率为 ,则直线
,则直线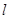 的方程为:
的方程为: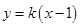 ,代入
,代入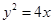 ,得:
,得: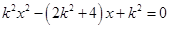 ,
,由根与系数的关系得:
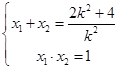 ,
,
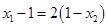 ,
,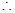
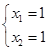 或
或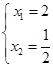 ,
,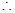
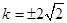 ,
,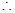 直线
直线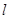 的方程为:
的方程为: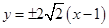 . ……12分
. ……12分点评:直线与圆锥曲线的位置关系是考查的重点内容也是常考的内容,思路不难,但是运算量比较大,而且根与系数的关系经常用到,应该加强训练.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

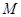 的坐标为
的坐标为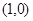 ;
;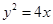 的焦点F,直线l过点
的焦点F,直线l过点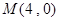 。
。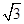 ,求直线l的斜率;
,求直线l的斜率;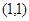 的抛物线的标准方程是 .
的抛物线的标准方程是 .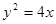 及点
及点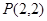 ,直线
,直线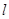 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。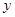 轴上截距的取值范围;
轴上截距的取值范围;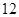 点时,拱顶离水面
点时,拱顶离水面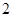 米,桥下的水面宽
米,桥下的水面宽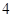 米;下午
米;下午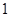 米,桥下的水面宽 米.
米,桥下的水面宽 米.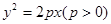 上一点
上一点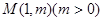 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线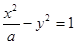 的左顶点为
的左顶点为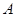 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线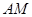 平行,则实数
平行,则实数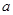 的值是( )
的值是( )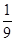
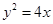 的焦点
的焦点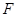 的直线交抛物线于
的直线交抛物线于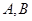 两点,点
两点,点 是原点,若
是原点,若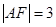 ,则
,则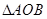 的面积为( )
的面积为( )