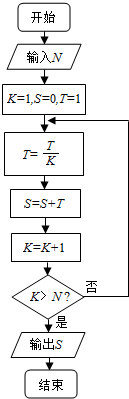
题目内容

8．在等差数列{an}中，a9=$\frac{1}{2}$a12+6，则该数列的前11项和为132．

分析 由已知结合等差数列的性质求得a6，再由S11=11a6求得答案．

解答 解：在等差数列{an}中，由a9=$\frac{1}{2}$a12+6，得
2a9-a12=12，即2a1+16d-a1-11d=12，∴a1+5d=a6=12，
则S11=11a6=11×12=132．
故答案为：132．

点评 本题考查了等差数列的性质，考查了等差数列的前n项和，是基础的计算题．

练习册系列答案
相关题目
18．已知△ABC是半径为5的圆O的内接三角形，且$tanA=\frac{4}{3}$，若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}（x、y∈R）$，则x+y的最大值为（　　）
A．$\frac{4}{3}$B．$\frac{{2\sqrt{3}}}{3}$C．1D．$\frac{5}{8}$
19．执行如图所示的程序框图，如果输出的S值大于$\frac{5}{3}$，则输入的正整数N的最小值为（　　）
A．4B．5C．6D．7
16．已知曲线C的极坐标方程是ρ=4cosθ．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=a+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.（t$是参数）．
（Ⅰ）写出曲线C的普通方程；
（Ⅱ）若直线l与曲线C相交于A、B两点，且|AB|=$\sqrt{14}$，求a的值．
3．执行如图所示的程序框图，若输入x=30，则输出的结果为（　　）
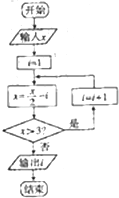
A．4B．3C．2D．1
13．已知复数z=$\frac{2}{1-i}$+i（i是虚数单位），则|z|=（　　）
A．1B．$\sqrt{3}$C．2D．$\sqrt{5}$
20．已知曲线C的极坐标方程是ρ=4cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t+1}\\{y=\frac{1}{2}t}\end{array}\right.$（t为参数）；
（1）求曲线C的直角坐标方程和直线l的普通方程；
（2）已知点P（1，0），若直线l与曲线C交于A，B两点，求|PA|•|PB|的值．
17．我们把焦点相同且离心率互为倒数的椭圆和双曲线称为一对“合一曲线”，已知F1，F2是一对“合一曲线”的焦点，P是他们在第一象限的交点，当|PF1|=10，|PF2|=8时，这一对“合一曲线”中椭圆的离心率为$\frac{1}{3}$．
18．能够把椭圆$\frac{{x}^{2}}{4}$+y2=1的周长和面积同时分为相等的两部分的函数称为椭圆的“可分函数”，下列函数不是椭圆的“可分函数”为（　　）
A．f（x）=4x3+xB．f（x）=ln$\frac{5-x}{5+x}$C．f（x）=sin$\frac{x}{2}$D．f（x）=ex+e-x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网