题目内容
9.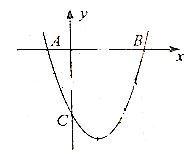 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.(1)求二次函数的表达式;
(2)在该函数图象上能否找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由.
分析 (1)由已知中二次函数y=ax2+bx-3的图象过坐标(-2,5),(3,0),代入构造方程,解方程求出a,b的值可得二次函数的表达式;
(2)若∠POC=∠PCO,则PC=PO,根据垂直平分线上的点到线段两端点的距离相等,结合二次函数解析式可求出P点坐标.
解答 解:(1)∵二次函数y=ax2+bx-3的图象过坐标(-2,5),(3,0),
∴$\left\{\begin{array}{l}4a-2b-3=5\\ 9a+3b-3=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=1\\ b=-2\end{array}\right.$
故二次函数的表达式y=x2-2x-3
(2)若∠POC=∠PCO,则PC=PO,
则P点在OC的垂直平分线上,
由(1)得C点坐标为(0,-3),
故OC的垂直平分线方程为:y=-$\frac{3}{2}$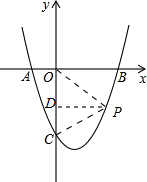
由x2-2x-3=-$\frac{3}{2}$得:x=$\frac{2±\sqrt{10}}{2}$,
故P点的坐标为:($\frac{2-\sqrt{10}}{2}$,-$\frac{3}{2}$),或($\frac{2+\sqrt{10}}{2}$,-$\frac{3}{2}$)
点评 本题考查的知识点是二次函数的图象和性质,函数解析式的求法,难度不大,属于基础题.

练习册系列答案
相关题目
18.已知△ABC是半径为5的圆O的内接三角形,且$tanA=\frac{4}{3}$,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,则x+y的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | 1 | D. | $\frac{5}{8}$ |
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).